Симплекс метод или метод последовательного уточнения оценок

Метод предназначен для решения общей задачи линейного программирования.

Пусть имеем следующую задачу:

,

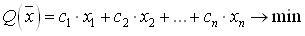с системой ограничений следующего вида:

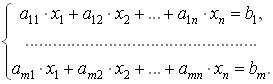
Разрешим эту систему относительно переменных x₁,...x_m:

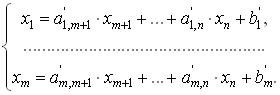(7.3)

Векторы условий, соответствующие x₁,...x_m, образуют базис. Переменные x₁,...x_m назовем базисными переменными. Остальные переменные задачи - небазисные.

Целевую функцию можно выразить через небазисные переменные:

.

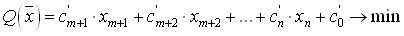Если приравнять небазисные переменные нулю

,

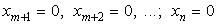то соответствующие базисные переменные примут значения

.

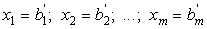Вектор 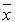с такими компонентами представляет собой угловую точку многогранника решений (допустимую) при условии, что b_i' ≥ 0 (опорный план).

Теперь необходимо перейти к другой угловой точке с меньшим значением целевой функции. Для этого следует выбрать некоторую небазисную переменную и некоторую базисную так, чтобы после того, как мы "поменяем их местами", значение целевой функции уменьшилось. Такой направленный перебор в конце концов приведет нас к решению задачи.

Достоинства – при нескольких модификациях является универсальным методом решения ЗЛП.

в) Двойственный симплекс-метод. Применяется когда исходную задачу сложнее решить, чем двойственную.

2-я теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов

при соответствующих переменных линейной функции исходной задачи, выраженной через неосновные переменные ее оптимального решения. На этой теореме основан двойственный симплекс-метод.

2) Задача нелинейного программирования (ЗНП)

,

,

,

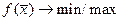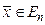
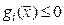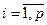
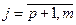
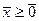
Универсальных методов таких задач не существует. Эффективные алгоритмы удалось разработать лишь для некоторых классов таких задач: задача дробно-линейного программирования, задача квадратичного программирования, задачи с линейной целевой функцией, задачи с линейными ограничениями и т.п.

Можно рассмотреть метод решения задач с линейными ограничениями и нелинейной целевой функцией – метод Франка-Вульфа.