
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы решения систем линейных алгебраических уравнений
Аппроксимация – приближение.
Разностная схема – совокупность разностных уравнений аппроксимирующих исходные дифференциальные уравнения. Используется для решения ДУ 1-го и 2-го порядка, а также уравнений в частных производных.
Метод прогонки – метод решения системы линейных уравнений с трех диагональной матрицей (не нулевые значения стоят по диагонали, под и над ней). Встречается в дифференциальных уравнениях 2-го порядка.
Решаем краевую задачу (граничные условия) (2.11) и (2.12). Заменяем дифференциальное уравнение разностной схемой, которая представляет собой линейную систему с трех диагональной матрицей. Метод прогонки используется в уравнениях мат. физики – заменяем, строим разностную схему с трех диагональной матрицей. Решение системы представляется в виде (2.14) и (2.15)
Рассмотрим систему линейных уравнений

Это система с трехдиагональной матрицей размерности  .
.

Для решения систем такого вида используется метод исключения неизвестных, называемый методом прогонки.
Пусть имеет место соотношение
 (2.13)
(2.13)
с неопределенными коэффициентами 
Подставим 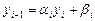 в (2.10), получаем
в (2.10), получаем
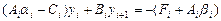
Сравнивая это тождество с (2.13), находим
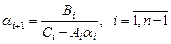 (2.14)
(2.14)
 (2.15)
(2.15)
Из (2.13) при i = 0 и (2.11) получаем
 (2.16)
(2.16)
Зная 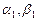 и переходя от i к i+1 в формулах (2.14) и (2.15) можно определить
и переходя от i к i+1 в формулах (2.14) и (2.15) можно определить  для
для 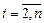 . Вычисление по формуле (2.13) ведутся путем перехода от i+1 к i (т.е. зная
. Вычисление по формуле (2.13) ведутся путем перехода от i+1 к i (т.е. зная  можно найти
можно найти  ) и для начала этих вычислений необходимо знать
) и для начала этих вычислений необходимо знать 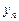 . Определим
. Определим 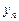 из (2.12) и (2.13) при i = n-1
из (2.12) и (2.13) при i = n-1
 (2.17)
(2.17)
Т.о., решение системы (2.10) – (2.12) методом прогонки, осуществляется по следующим формулам: Прямой ход:

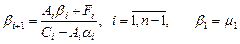
Обратный ход:

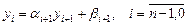
Дата добавления: 2015-04-18; просмотров: 239; Мы поможем в написании вашей работы!; Нарушение авторских прав |