Необходимое и достаточное условие дифференцируемости

Теорема . Для того, чтобы функция f(x) была дифференцируема в точке x₀, необходимо и достаточно, чтобы в этой точке она имела конечную производную.

Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке.

б) Прямые методы.

Достоинства – не требуют вычисления производных функции, функция не обязательно должна быть задана в аналитическом виде.

Представители: метод случайного поиска, метод случайных направлений, метод случайных направлений с возвратом при неудачном шаге.

Недостаток: плохая сходимость.

в) Методы, использующие производные функции.

Достоинтсва – высокая скорость сходимости по сравнению с прямыми методами.

Представитель: метод градиентного спуска. Градиент показывает направление скорейшего убывания функции.

Задача многомерной оптимизации при наличии ограничений

Постановка задачи

,

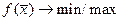
Задачи математического программирования

1) Задача линейного программирования (ЗЛП)

,

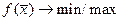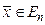
Ограничения(равенства и неравенства):

,

,

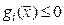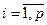
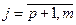
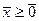
Методы решения

а) Графический метод.

Геометрический метод применяется, если задача линейного программирования содержит только две переменные. Рисуем область допустимых решений и график целевой функции. Сдвигаем график целевой функции параллельным переносом в направлении ее вектора нормали (для задач максимизации) или в противоположном направлении (для задач минимизации). Последняя общая точка сдвинутого графика целевой функции и области допустимых решений и есть решение задачи. Возможно, что график совпадает с одним из отрезков, ограничивающих допустимую область решений. В этом случае решений будет бесконечно много.

Достоинства – простота, наглядность. Недостатки – ограниченность применения.

б) Симплекс-метод.