
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы бучения без учителя
Главная черта, делающая обучение без учителя привлекательным, - его "самостоятельность". Процесс обучения, как и в случае обучения с учителем, заключается в подстраивании весов синапсов. Некоторые алгоритмы, правда, изменяют и структуру сети, то есть количество нейронов и их взаимосвязи, но такие преобразования правильнее назвать более широким термином – самоорганизацией.
Очевидно, подстройка синапсов может проводиться только по информации, доступной в нейроне, то есть его состоянию и уже имеющимся весовым коэффициентам. Эта идея и, что более важно, аналогия с известными принципами самоорганизации нервных клеток дали основу алгоритмов обучения Хебба.
Сигнальный метод обучения Хебба заключается в изменении весов по следующему правилу:
 , (1)
, (1)
где: yi(n-1) – выходное значение нейрона i слоя (n-1), yj(n) - выходное значение нейрона j слоя n; wij(t) и wij(t-1) - весовой коэффициент синапса, соединяющего эти нейроны, на итерациях t и t-1 соответственно; h - коэффициент скорости обучения. Здесь и далее, для общности, под n подразумевается произвольный слой сети. При обучении по данному методу усиливаются связи между возбужденными нейронами.
Существует также и дифференциальный метод обучения Хебба.
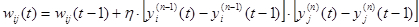 . (2)
. (2)
Здесь yi(n-1)(t) и yi(n-1)(t-1) - выходное значение нейрона i слоя n-1 соответственно на итерациях t и t-1; yj(n)(t) и yj(n)(t-1) - то же самое для нейрона j слоя n. Сильнее всего обучаются синапсы, соединяющие те нейроны, выходы которых наиболее динамично изменились в сторону увеличения.
Полный алгоритм обучения с применением вышеприведенных формул будет выглядеть так:
1. На стадии инициализации всем весовым коэффициентам присваиваются небольшие случайные значения.
2. На входы сети подается входной образ, и сигналы возбуждения распространяются по всем слоям согласно принципам классических прямопоточных (feedforward) сетей, то есть для каждого нейрона рассчитывается взвешенная сумма его входов, к которой затем применяется активационная (передаточная) функция нейрона, в результате чего получается его выходное значение yi(n), i = 0, ..., Mi-1, где Mi - число нейронов в слое i; n = 0, ..., N-1, а N - число слоев в сети.
3. На основании полученных выходных значений нейронов по формуле (1) или (2) производится изменение весовых коэффициентов.
4. Цикл с шага 2, пока выходные значения сети не застабилизируются с заданной точностью. Применение этого нового способа определения завершения обучения, отличного от использовавшегося для сети обратного распространения, обусловлено тем, что подстраиваемые значения синапсов фактически не ограничены. На втором шаге цикла попеременно предъявляются все образы из входного набора.
Следует отметить, что вид откликов на каждый класс входных образов не известен заранее и будет представлять собой произвольное сочетание состояний нейронов выходного слоя, обусловленное случайным распределением весов на стадии инициализации. Вместе с тем, сеть способна обобщать схожие образы, относя их к одному классу. Тестирование обученной сети позволяет определить топологию классов в выходном слое. Для приведения откликов обученной сети к удобному представлению можно дополнить ее слоем, который, например, по алгоритму обучения однослойного перцептрона будет отображать выходные реакции сети в требуемые образы.
Полный алгоритм обучения имеет примерно такую же структуру, как в методах Хебба, но на шаге 3 из всего слоя выбирается нейрон, значения синапсов которого максимально походят на входной образ, и подстройка весов по формуле (3) проводится только для него. Эта так называемая аккредитация может сопровождаться затормаживанием всех остальных нейронов слоя и введением выбранного нейрона в насыщение. Выбор такого нейрона может осуществляться, например, расчетом скалярного произведения вектора весовых коэффициентов с вектором входных значений. Максимальное произведение дает выигравший нейрон.
Другой вариант - расчет расстояния между этими векторами в p-мерном пространстве, где p - размер векторов.
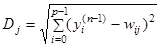 , (3)
, (3)
где: j - индекс нейрона в слое n, i - индекс суммирования по нейронам слоя (n-1), wij - вес синапса, соединяющего нейроны; выходы нейронов слоя (n-1) являются входными значениями для слоя n. Корень в формуле (4.41) брать не обязательно, так как важна лишь относительная оценка различных Dj. В данном случае "побеждает" нейрон с наименьшим расстоянием. Иногда слишком часто получающие аккредитацию нейроны принудительно исключаются из рассмотрения, чтобы "уравнять права" всех нейронов слоя. Простейший вариант такого алгоритма заключается в торможении только что выигравшего нейрона.
На основании рассмотренного выше метода строятся нейронные сети особого типа – так называемые самоорганизующиеся структуры – self-organizing feature maps. Для них после выбора из слоя n нейрона j с минимальным расстоянием Dj (3) обучается по формуле (4.40) не только этот нейрон, но и его соседи, расположенные в окрестности R. Величина R на первых итерациях очень большая, так что обучаются все нейроны, но с течением времени она уменьшается до нуля. Поэтому, чем ближе конец обучения, тем точнее определяется группа нейронов для каждого класса образов.
Дата добавления: 2015-04-18; просмотров: 217; Мы поможем в написании вашей работы!; Нарушение авторских прав |