Погрешность функции измеренных величин. Прогнозирование влияния систематической погрешности при ОМС по 2ЛП.

Основная теорема теории погрешностей
В геодезической практике мы, как правило, имеем дело не с непосредственно измеренными величинами, а с их функциями, т.е. косвенными измерениями.
Так, уклон линии определяют как отношение непосредственно измеренных превышения и длины линии. Длину линии, недоступной для непосредственного измерения, находят из решения треугольника, где непосредственно измерены базисная сторона и горизонтальные углы. Площадь земельного участка прямоугольной формы вычисляют как произведение непосредственно измеренных длины и ширины участка. Перечень подобных примеров можно продолжить. Отсюда возникает задача оценки точности функции измеренных величин по известным стандартам ? или средним квадратическим погрешностям m непосредственно измеренных аргументов

Предельная погрешность

С помощью закона Гаусса можно показать, что при достаточно большом числе измерений случайная погрешность измерения может быть:

Больше средней квадратической примерно в 32 случаях из 100;

Больше удвоенной средней квадратической только в 5 случаях из 100;

Больше утроенной средней квадратической лишь в 3 случаях из 100.

Следовательно, маловероятно, чтобы случайная погрешность измерения получилась больше утроенной средней квадратической. Поэтому утроенную среднюю квадратическую погрешность считают предельной:

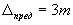
(5)

Теперь все чаще в геодезии за предельную ошибку принимают не утроенную (формула 5), а удвоенную среднюю квадратическую ошибку с риском ошибиться на 5%.

Если в ряду случайных ошибок встречается ошибка по абсолютному значению больше предельной для данного ряда, то такую ошибку считают грубой.

2.4 Оценка радиальной погрешности ОМС по 2 ЛП

1. Радиальная СКП обсервованного места судна оценивается по формуле:

М0 = cosecÖ m2 лп1 + m2лп2 = 0,0997 (мили)

где М0 - радиальная СКП обсервованного места судна

2. По отношениям полуосей эллипса погрешностей, заданной и радиальной СКП с помощью табл. 1-в МТ-75 определяем вероятность нахождения судна в круге радиальной СКП P(M0):

e = в/a Мзад = М0 R = Мзад/М0 = М0/М0 = 1

P(M0) = 66,3%

3. С помощью табл. 1-в МТ-75 определяем радиальные погрешности возможного места судна (Mзад) для заданных вероятностей: P(Mзад) = 0,95; P(Mзад) = 0,99:

Для P(Mзад) = 0,95 R = 1,7 Mзад = 0,46 (мили)

Для P(Mзад) = 0,99 R = 2,2 Mзад = 0,6 (мили)