Упражнение4.5.

1) Функция 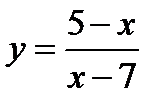является элементарной. Из теоремы 4.6 следует, что она непрерывна всюду в области своего задания 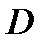. Знаменатель не должен обращаться в ноль, поэтому . Проверяем условия непрерывности в точке . Значения в этой точке функция не имеет. Вычисляем левый предел (см. замечание к теореме (4.3))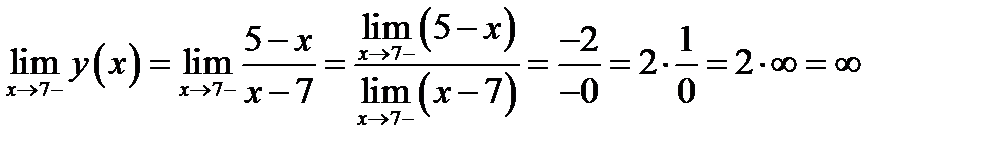

Вычисляем правый предел (см. замечание к теореме (4.2))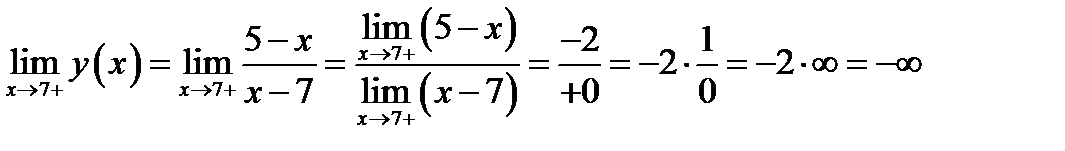

Ответ.Функция непрерывна всюду при 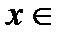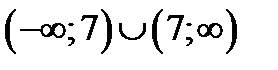. В точке бесконечный разрыв.

2) Функция является элементарной. Из теоремы 4.6 следует, что она непрерывна всюду в области своего задания 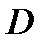. Знаменатель не должен обращаться в ноль, поэтому 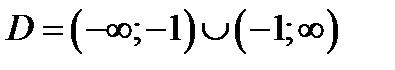. Ответ. Функция непрерывна всюду при . В точке 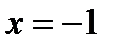бесконечный разрыв.

3)Функция непрерывна всюду при .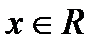

4) Функция является элементарной . Из теоремы 4.6 следует, что она непрерывна всюду в области своего задания 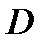. Знаменатель не должен обращаться в ноль, поэтому единственная точка подозрительная на разрыв это точка .

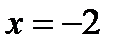Проверяем условия непрерывности в этой точке. Значения в этой точке функция не имеет. Вычисляем левый предел

.

Вычисляем правый предел

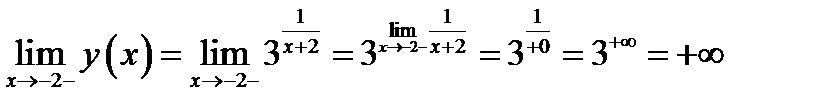
Ответ. Функция непрерывна при . Функция в точке 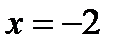терпит бесконечный разрыв справа.

5) Функция 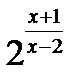непрерывна при 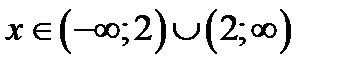. Функция в точке терпит бесконечный разрыв справа.

6) Функция непрерывна при . Функция в точке

терпит устранимый разрыв.