Упражнение 4.7.

3) , 5). Сформулируйте теорему, которую использовали при решении этой задачи.

Упражнение 4.8. По аналогии с решением упражнения 4.6 функция

непрерывна на интервалах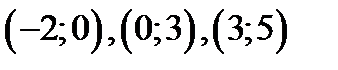

Исследуем функцию на непрерывность в пограничных точках .

Для точки проверяем условие непрерывности . Следовательно, в точке функция непрерывна.

Для точки проверяем условие непрерывности

В точке функция непрерывна.

Для точки 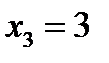проверяем условие непрерывности

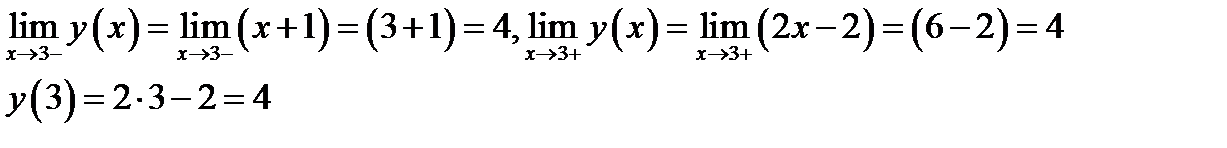
В точке 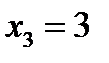функция непрерывна.

Для точки 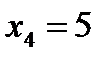проверяем условие непрерывности

В точке 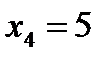функция непрерывна. Строим эскиз графика

Таким образом , данная функция непрерывна на замкнутом отрезке . Следовательно у неё на этом отрезке существует минимальное значение и максимальное значение .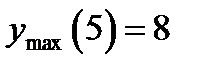

2) 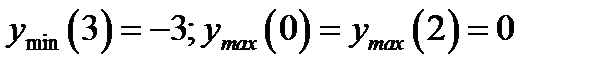, 3) ;

4) .

Упражнение 4.13. 1) Наибольшего значения нет, наименьшее .

2) Наибольшее значение , наименьшее .

Замечательные пределы.