Упражнение 4.6.

1) Функция 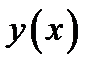непрерывна на интервалах 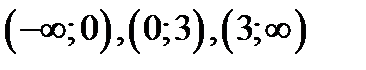, где она задана элементарными функциями. Разрыв возможен только в пограничных точках 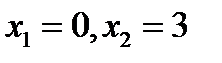. Для этого нужно проверить равенства

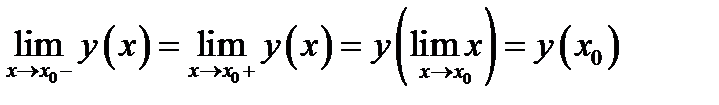(4.5)

Проверяем условия непрерывности в точке 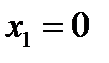. Вычисляем левый предел.

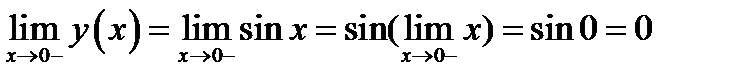. Вычисляем правый предел Значение функции в точке 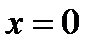вычисляется по формуле . Вывод. Функция в точке 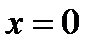терпит разрыв скачок.

Проверяем условия непрерывности в точке 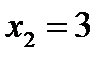. Вычисляем левый предел.

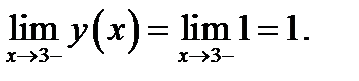Вычисляем правый предел 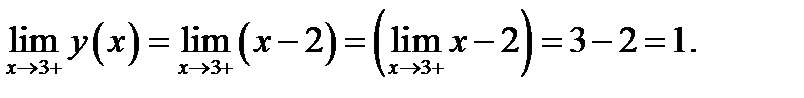Значение функции в точке 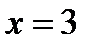вычисляется по формуле 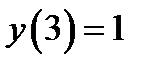. Так как левое предельное значение равно правому предельному значению и равно значению функции, то в точке 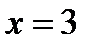функция непрерывна.

Ответ. Функция 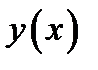непрерывна на множестве 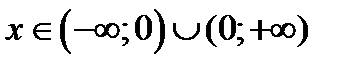. В точке 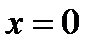разрыв -скачок. Эскиз графика строим по точкам (рис.1)

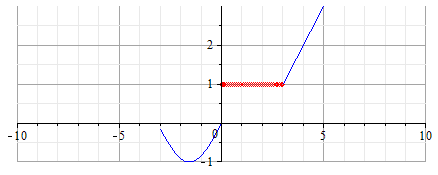
рис.1

2) Функция непрерывна на множестве ;

3) Функция непрерывна на множестве 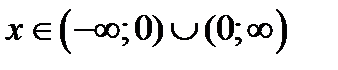; В точке 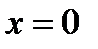имеется разрыв-скачок.

4) Функция непрерывна на множестве 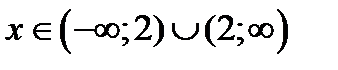; В точке 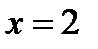имеется разрыв-скачок.