
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Агроинженерия 1 страница
Рухленко А.П.
ГИДРАВЛИКА
Примеры решения задач
Учебно-методическое пособие
Для подготовки бакалавров по направлению
Агроинженерия
Тюмень – 2012
УДК 621.22
БКК 31.56
Г 46
Рецензент:
кандидат технических наук, доцент А. Е. Королев.
Автор-составитель: А. П. Рухленко, кандидат технических наук, доцент.
Г 46 Рухленко А. П. Гидравлика. Примеры решения задач ТюмГСХА. - Тюмень, 2012.
Приведены примеры решения задач по всем основным разделам дисциплины. Пособие содержит 57 задач с подробным пояснением решения каждой.
Назначение данного пособия- помочь студентам в самостоятельном изучении и усвоении методики решения задач по всем темам курса.
Печатается по решению методической комиссии Механико-технологического института ТГСХА.
© Тюменская Государственная
Сельскохозяйственная академия.
© А. П. Рухленко, 2012.
Предисловие
Важным условием усвоения студентами теоретического курса является умение использовать знания теоретических основ при решении конкретных инженерных задач. Именно решение задач развивает у студентов навыки к творческому инженерному мышлению, способствует развитию самостоятельности при решении инженерных вопросов, связанных с изучением этой дисциплины.
Все задачи в данном пособии размещены в порядке изучения дисциплины по тематикам, согласно рабочим программам по подготовке бакалавров направления 110800- агроинженерия.
Пособие предназначено для студентов очной и заочной формы обучения. Цель его – помочь студентам освоить методику решения задач по темам курса «Гидравлика». Особенно полезно, по мнению автора, пособие будет для студентов, пропускающих занятия, ибо оно поможет им в освоении данной дисциплины.
В таблице, приведенной ниже, указываются номера задач по каждой теме и литература для изучения теоретического материала по каждой теме.
Тематика практических занятий
по решению задач
| Тема занятия | №№ задач по теме | Литература, стр. № | ||||
| Физичес-кие свойства жидкостей | 1,2 | 8..13 | 8..14 | 7..12 | 3..4 | 3…4 |
| Гидроста-тическое давление | 3,4,5,6,7,8, | 20..25 | 19..25 | 17..20 | 5..7 | 7..8 |
| Сила гидростати-ческого давления на плоские и криволи-нейные поверх-ности | 9,10,11,12,13,14, 15,16,17,19,21 | 25..31 | 28..34 | 21..27 | 7..9 | 15..16 |
| Уравнение Бернулли. Гидравли-ческие сопротив-ления | 22,23,24,25,26,27 28,29,30,31,32 | 42..45 55..64 | 46..52 52..78 | 44..59 | 13..16 19..24 | 30..36 |
| Истечение жидкости через отверстия, насадки, дроссели и клапаны | 34,35,36,37,38,39, 40,41 | 72..79 | 78..89 | 63..76 | 25..29 | 45..48 |
| Гидравли-ческий расчет трубопро-водов | 42,43,44 | 64..70 | 94..104 | 76..99 | 31..38 | 57..63 |
| Лопастные насосы | 45,46,47,48 | 89..108 131..134 | 139..158 163..173 | 146..161 | 41..59 | 78..83 |
| Объемные гидрома-шины | 50,51,52,53 | 141..169 | 177..204 | 223..235 | 59..76 | 88..91 |
| Объемный гидропри-вод | 54,55,56,57 | 192..200 | 204..224 | 271..279 | 77..84 | 95..98 |
Литература для изучения теоретической части дисциплины
1. Исаев А.П., Сергеев Б.И., Дидур В.А. Гидравлика и гидромеханизация сельскохозяйственных процессов М:Агропром издат, 1990 – 400с.
2. Н.А.Палишкин Гидравлика и сельскохозяйственное водоснабжение М: Агропром издат, 1990 - 351с.
3. Сабащвили Р.Г. Гидравлика, гидравлические машины, водоснабжение сельского хозяйства: Учеб. пособие для вузов М: Колос 1997-479с.
4. Рухленко А.П. Гидравлика и гидравлические машины. Учебное пособие ТГСХА-Тюмень 2006 г. 124с.
 1. Определить объемный модуль упругости жидкости,
1. Определить объемный модуль упругости жидкости,
если под действием груза А массой 250 кг поршень прошел расстояние △h=5мм. Начальная высота положения поршня H=1.5м, диаметры поршня d=80мм и резервуара D=300мм, высота резервуара h=1,3 м. Весом поршня пренебречь. Резервуар считать абсолютно жестким.
Решение: Сжимаемость жидкости характеризуется модулем объемной упругости Е, входящим в обобщенный закон Гука:  =
=  ,
,
где  = приращение (в данном случае уменьшение) объема жидкости V , обусловленное увеличением давления ∆р. Вышеприведенную зависимость запишем относительно искомой величины:
= приращение (в данном случае уменьшение) объема жидкости V , обусловленное увеличением давления ∆р. Вышеприведенную зависимость запишем относительно искомой величины:
E =  .
.
В правой части уравнения неизвестные величины необходимо выразить через исходные данные. Повышение давления ∆робусловленное внешней нагрузкой, а именно весом груза:
E = 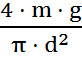 .
.
Начальный объем жидкости складывается из объемов жидкости в цилиндре и резервуаре:
 =
=  ·
·  .
.
Абсолютное изменение объема жидкости ∆V :
 =
=  ·
·  .
.
Подставив в правую часть уравнения полученные выражения для ∆р, ∆V и V получим
E =  =
=
=  =
=  .
.
 2. Высота цилиндрического вертикального резервуара h=10м, его диаметр D=3м. Определить массу мазута (ρм=920кг/
2. Высота цилиндрического вертикального резервуара h=10м, его диаметр D=3м. Определить массу мазута (ρм=920кг/  ), которую можно налить в резервуар при 15
), которую можно налить в резервуар при 15  , если его температура может подняться до 400С. Расширением стенок резервуара пренебречь, температурный коэффициент объемного расширения жидкости βt=0,0008 1/0С.
, если его температура может подняться до 400С. Расширением стенок резервуара пренебречь, температурный коэффициент объемного расширения жидкости βt=0,0008 1/0С.
Решение: Массу мазута можно выразить как произведение его плотности на объем, т. е.:
 или
или 

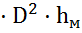 ,
,
где hм - начальный уровень мазута в резервуаре при t=150С. Из выражения для βt находим абсолютное изменение объема мазута при повышении температуры, т.е.:
 .
.
С другой стороны, эту же величину можно представить как разность объемов резервуара и начального объема мазута:
V = 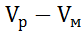 .
.
Выразив эти объемы через геометрические параметры можно записать, что:
ΔV =  ·
· 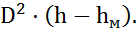
Приравняем правые части выражений для  :
:




 .
.
Сократив левую и правую части уравнения на  , получим
, получим
 , откуда
, откуда  =
=  .
.
Полученное значение 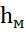 подставим в исходное уравнение
подставим в исходное уравнение
 =
=
= 63700кг.
Здесь: △t = tk - tн = 40 – 15 = 250С.
 3. Определить абсолютное давление воздуха в баке
3. Определить абсолютное давление воздуха в баке 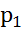 , если при атмосферном давлении, соответствующем ha = =760 мм рт. ст. показание ртутного вакуумметра
, если при атмосферном давлении, соответствующем ha = =760 мм рт. ст. показание ртутного вакуумметра 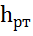 = 0,2 м, высота h = 1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути ρ = 13600кг/
= 0,2 м, высота h = 1,5 м. Каково при этом показание пружинного вакуумметра? Плотность ртути ρ = 13600кг/  .
.
Решение: Для решения этой задачи используем основное уравнение гидростатики, позволяющее определить давление в любой точке жидкости и понятие «поверхность равного давления». Как известно, для неподвижной ньютоновской жидкости поверхности равного давления представляют совокупность горизонтальных плоскостей. В данном случае в качестве поверхностей равного давления возьмем две горизонтальные плоскости - поверхность раздела воды и воздуха в соединительной трубке и поверхность раздела воздуха и ртути в правом колене ртутного вакуумметра. Для первой поверхности давление в точках А и В одинаково и согласно основного уравнения гидростатики определяется следующим образом:
pА = pВ = p1 + ρ · g · h ,
где р1 - абсолютное давление воздуха в баке. Из этого уравнения следует , что:
p1 = pA - ρ · g · h.
Если не учитывать плотность воздуха, то можно записать что pА = pВ = pЕ, т.е. давления в точках А,В, и Е одинаковы.
Для второй поверхности давления в точках С и Д одинаковы и равны атмосферному,
ра = рС = рД.
С другой стороны, давление в т. С можно представить как

откуда pе = pа – ρрт·g · hрт.
Подставив выражения для рА в уравнение для определения р1, получим
р1 = pa - ρрт · g · hрт – ρ · g · h = ρрт · g · (ha - hрт) – ρ · g · h.
Численную величину р1 найдем, подставив численные значения величин в правой части уравнения:
р1 = 13600 · 9,81 · (0,76 – 0,2) – 1000 · 9,81 · 1,5=
= 74713 – 14715 = 59998Па = 60кПа.
Разрежение, которое будет показывать вакуумметр:
рвак = ра – р1 = ρрт · g · hа – р1=
=13600 · 9,81 · 0,76 · 10-3- 60 = 101,4 – 60 = 41,4кПа.
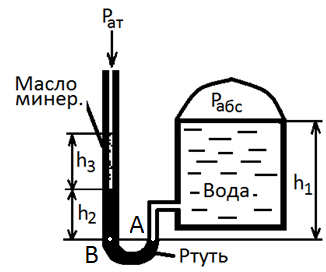 4.Определить абсолютное давление в сосуде по показанию жидкостного манометра, если известно: h1=2м, h2=0,5м, h3=0,2м,
4.Определить абсолютное давление в сосуде по показанию жидкостного манометра, если известно: h1=2м, h2=0,5м, h3=0,2м,  м= = 880кг/м3.
м= = 880кг/м3.
Решение: Для решения этой задачи необходимо записать основное уравнение гидростатики для двух точек, распложенных на горизонтальной плоскости (поверхности равного давления), проходящей по линии раздела воды и ртути . Давление в т. А
рА = рабс + ρ · g · h1;
Давление в т. В
рВ  .
.
Приравняв правые части этих выражений определим абсолютное давление
рабс + ρ · g · h1 = ра + ρм · g · h3 + ρрт · g · h2,
откуда
 =
=
=100000+880·9,81·0,2+13600·9,81·0,5–1000·9,81·2 =
=100000+1726,6+66708-19620=148815Па=148кПа.
 5. Закрытый резервуар А, заполненный керосином на глубину Н=3м, снабжен вакуумметром и пьезометром. Определить абсолютное давление р0 над свободной поверхностью в резервуаре и разность уровней ртути в вакуумметре h1 если высота поднятия керосина в пьезометре h =1,5м.
5. Закрытый резервуар А, заполненный керосином на глубину Н=3м, снабжен вакуумметром и пьезометром. Определить абсолютное давление р0 над свободной поверхностью в резервуаре и разность уровней ртути в вакуумметре h1 если высота поднятия керосина в пьезометре h =1,5м.
Решение: Запишем основное уравнение гидростатики для т. А, расположенной на дне резервуара,
 ,
,
откуда
 .
.
С другой стороны, это же давление в точке А можно выразить через показание открытого пьезометра
 .
.
Полученное выражение для рА вставим в уравнение для определения р0:
 .
.
Примем  ,
,
тогда численное значение р0 будет равно:
 .
.
Разность уровней ртути в вакууметре определим, записав основное уравнение гидростатики для двух точек В и С поверхности равного давления, совпадающей со свободной поверхностью ртути в правом колене вакуумметра

откуда
h1 =  =
= 
 .
.
 6. Определить избыточное давление воды в трубе В, если показание манометра
6. Определить избыточное давление воды в трубе В, если показание манометра  =0,025МПа.
=0,025МПа.
Соединительная трубка заполненная водой и
воздухом , как показано на схеме, причем Н1 = 0,5м, Н2 =3м. Как изменится показание манометра , если при том же давлении в трубе всю соединительную трубку заполнить водой (воздух выпустить через кран К). Высота 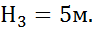
Решение: При решении этой задачи используется основное уравнение гидростатики, согласно которому, давление в трубе В, складывается из давления на свободной поверхности (в данном случае манометрического - рм) и весового давления воды. Воздух в расчет не принимается ввиду его малой, сравнительной с водой, плотности.
Итак давление в трубе В:
 =
=

Здесь  1 взято со знаком минус, потому что этот столб воды способствует уменьшению давления в трубе.
1 взято со знаком минус, потому что этот столб воды способствует уменьшению давления в трубе.
Если из соединительной трубки полностью удалить воздух, то в этом случае основное уравнение гидростатики запишется так:

откуда
 .
.
Точное значение ответов:  и
и 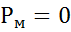 получается при g = 10 м/
получается при g = 10 м/  .
.
 7. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине Н=5м, если показание вакуумметра, установленного на высоте h=1.7м,
7. При перекрытом кране трубопровода К определить абсолютное давление в резервуаре, зарытом на глубине Н=5м, если показание вакуумметра, установленного на высоте h=1.7м,  . Атмосферное давление соответствует
. Атмосферное давление соответствует  Плотность бензина
Плотность бензина  .
.
Решение: Согласно основному уравнению гидростатики абсолютное давление в резервуаре будет складываться из абсолютного давления на свободной поверхности и весового, т. е.
 .
.
Абсолютное давление на свободной поверхности  :
:
 или
или 
С учетом полученного выражения для
 исходное уравнение запишем следующим образом:
исходное уравнение запишем следующим образом: 



 8. В цилиндрический бак диаметром D = 2м до уровня Н=1,5м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h=300мм. Определить вес находящегося в баке
8. В цилиндрический бак диаметром D = 2м до уровня Н=1,5м налиты вода и бензин. Уровень воды в пьезометре ниже уровня бензина на h=300мм. Определить вес находящегося в баке
бензина, если 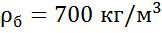 .
.
Решение: Вес находящегося в баке бензина можно записать как
 ,
,
где 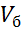 - объем бензина в баке. Выразим его через геометрические параметры бака:
- объем бензина в баке. Выразим его через геометрические параметры бака:
 .
.
Чтобы определить неизвестную величину  - уровень бензина в баке, нужно записать основное уравнение гидростатики для поверхности равного давления, в качестве которой наиболее целеобразно принять дно бака, так как относительно его мы располагаем информацией в виде Н- суммарного уровня бензина и воды в баке. Так как бак и пьезометр открыты (сообщаются с атмосферой), давление на дно будем учитывать только весовое.
- уровень бензина в баке, нужно записать основное уравнение гидростатики для поверхности равного давления, в качестве которой наиболее целеобразно принять дно бака, так как относительно его мы располагаем информацией в виде Н- суммарного уровня бензина и воды в баке. Так как бак и пьезометр открыты (сообщаются с атмосферой), давление на дно будем учитывать только весовое.
Итак, давление на дно со стороны бака можно записать как
 .
.
Это же давление со стороны пьезометра:
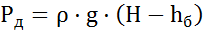 .
.
Приравняв правые части полученных выражений, выразим из них искомую величину  :
:
 .
.
Сократим полученное уравнение на g, убрав в обеих частях уравнения  , запишем искомую величину
, запишем искомую величину
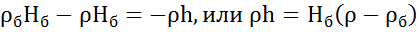 .
.
Из последнего уравнения

 .
.
Полученные выражения для  и
и 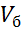 подставим в исходное уравение и определим вес бензина
подставим в исходное уравение и определим вес бензина
 =
= 


 =
=
 .
.
 9. Гидравлический домкрат состоит из неподвижного поршня 1 и скользящего по нему цилиндра 2, на котором смонтирован корпус 3, образующий масляную ванну домкрата и плунжерный насос 4 ручного привода со всасывающими 5 и нагнетательным 6 клапанами. Определить давление рабочей жидкости в цилиндре и массу поднимаемого груза m, если усилие на рукоятке приводного рычага насоса R=150 Н, диаметр поршня домкрата D=180 мм, диаметр плунжера насоса d=18мм, КПД домкрата η = 0,68, плечи рычага а=60мм, b=600мм.
9. Гидравлический домкрат состоит из неподвижного поршня 1 и скользящего по нему цилиндра 2, на котором смонтирован корпус 3, образующий масляную ванну домкрата и плунжерный насос 4 ручного привода со всасывающими 5 и нагнетательным 6 клапанами. Определить давление рабочей жидкости в цилиндре и массу поднимаемого груза m, если усилие на рукоятке приводного рычага насоса R=150 Н, диаметр поршня домкрата D=180 мм, диаметр плунжера насоса d=18мм, КПД домкрата η = 0,68, плечи рычага а=60мм, b=600мм.
Решение: Давление рабочей жидкости в цилиндре определяется как отношение силы, действующей на поршень, насоса к площади поршня и умноженное на КПД домкрата т. е.:
р =  ·
·  .
.
Сила, действующая на поршень определяется из уравнения моментов сил, действующих на рычаг насоса,
F = R ·  .
.
Площадь поршня насоса:
S = 
 .
.
Подставив значения силы и площади в начальное уравнение, получим
Р = 
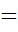

 Па = 4,01МПа.
Па = 4,01МПа.
Масса поднимаемого груза определяется из уравнения равномерного движения цилиндра относительно неподвижного поршня при подаче в цилиндр рабочей жидкости насосом
m · g = p · Sц,
откуда масса груза:
m =  =
=  =
=
= 
 .
.
 10. Покоящийся на неподвижном поршне и открытый сверху и снизу сосуд массой
10. Покоящийся на неподвижном поршне и открытый сверху и снизу сосуд массой
m=16 кг состоит из двух цилиндрических частей, внутренние диаметры которых равны D=0.5 м и d=0,3м. Определить, какой минимальный объем воды должен содержаться в верхней части сосуда, чтобы сосуд всплыл над поршнем. Трением сосуда о поршень пренебречь.
Решение: Объем воды в верхней части сосуда определяется через геометрические параметры

 ·
·  ,
,
где h - уровень воды в верхней части сосуда (в малом цилиндре).
Этот уровень можно определить записав уравнение равновесия цилиндра в момент перед его всплытием. На него действуют две силы: сила тяжести сосуда, направленная вниз, и сила давления заливаемой в сосуд воды т. е.
mg =  · g · h ·
· g · h ·  ·
·  ,
,
откуда
h = 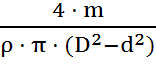 .
.
Подставив полученное выражение в начальное уравнение, получим искомый объем воды:
V =  =
=
 =
=  =
= 
 11. Определить значение силы, действующей на перегородку, которая разделяет бак, если ее диаметр D=0,5 м , показания вакуумметра pвак=0,08МПа,
11. Определить значение силы, действующей на перегородку, которая разделяет бак, если ее диаметр D=0,5 м , показания вакуумметра pвак=0,08МПа,
и манометра рм=0,1МПа.
Решение: Сила давления на перегородку определяется как произведение разности абсолютных давлений слева и справа от перегородки на её площадь, т.е:
F = ( 
где 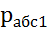 =(
=( 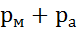 ) абсолютное давление справа от перегородки;
) абсолютное давление справа от перегородки;
 =
=  ,
,
абсолютное давление слева от перегородки;
 - площадь перегородки.
- площадь перегородки.
Таким образом, сила действующая на перегородку, запишется следующим образом:
F =  ,
,
или
F =  =
=

 .
.
12. Определить минимальную силу тяжести груза G который при заливке формы чугуном нужно положить на верхнею опоку, чтобы предотвратить
его всплывание. Вес верхней опоки  Плотность жидкого чугуна
Плотность жидкого чугуна  =7000кг/
=7000кг/  . Вес чугуна в литниках и выпорах не учитывать. Размеры: а=150 мм, в=150мм,
. Вес чугуна в литниках и выпорах не учитывать. Размеры: а=150 мм, в=150мм, 

Дата добавления: 2015-04-18; просмотров: 2292; Мы поможем в написании вашей работы!; Нарушение авторских прав |