
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Агроинженерия 2 страница
Решение: Для определения веса груза, который нужно положить на верхнею опоку во избежание ее всплытия необходимо записать уравнение равновесия опоки. На верхнюю опоку при заливке формы чугуном будут действовать три силы: вес груза и опоки, и сила давления жидкого чугуна, заливаемого в форму:
 .
.
Из этого уравнения вес груза
 .
.
В последнем уравнении неизвестна сила давления жидкого чугуна на опоку. Она определяется как произведение весового давления чугуна на смоченную поверхность (нижнюю) верхней опоки.
 =
=

Вес груза:

 .
.
13. Смотровой люк в боковой стенке резервуара перекрывается полусферической крышкой диаметром d=0,6 м. Определить отрывающее Fx усилия, и сдвигающее Fz, воспринимаемые болтами, если уровень бензина над центром отверстия Н=2 м. Показание манометра р=4.1кПа.
Решение: Отрывающее усилие Fх - это есть горизонтальная составляющая силы давления на полусферическую крышку. Как известно, горизонтальная составляющая равна силе давления на вертикальную проекцию этой полусферической крышки.
 =
=


Плотность бензина принята здесь равной  . Сдвигающее усилие Fz численно равно весу бензина, заключенного в полусферической крышке (вертикальная составляющая полной силы давления на крышку).
. Сдвигающее усилие Fz численно равно весу бензина, заключенного в полусферической крышке (вертикальная составляющая полной силы давления на крышку).
Fz = 

 14. Квадратное отверстие со стороной h=1м в вертикальной стенке резервуара закрыто плоским щитом. Щит закрывается грузом массой m, на плече х=1,3м. Определить величину массы груза, необходимую для удержания глубины воды в резервуаре Н=2,5 м, если величина а=0,5м.
14. Квадратное отверстие со стороной h=1м в вертикальной стенке резервуара закрыто плоским щитом. Щит закрывается грузом массой m, на плече х=1,3м. Определить величину массы груза, необходимую для удержания глубины воды в резервуаре Н=2,5 м, если величина а=0,5м.
Решение: Для удержания массы груза необходимо записать уравнение равновесие щита, которое будет представлять уравнение моментов, так как щит может совершать только поворотное движение т.е. ∑М0=0. На щит действуют два момента: момент силы тяжести груза и момент силы давления воды , т. е. можно записать, что
m·g·x=  ,
,
где  сила давления воды, а
сила давления воды, а 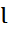 - плечо этой силы относительно оси поворота.
- плечо этой силы относительно оси поворота.
Сила давления воды:


Точка приложения этой силы относительно свободной поверхности воды в резервуаре:

 =
=

а плечо силы Fж определится следующим образом:

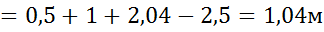 .
.
Из начального уравнения масса груза равна
m = 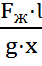 =
= 
 .
.
 15.Определить давление р1 жидкости, которую необходимо подвести к гидроцилиндру, чтобы преодолеть усилие, направленное вдоль штока F=1кН. Диаметры: цилиндра D=50мм, штока d=25мм. Давление в бачке р0=50кПа, высота Н0=5м. Cилу трения не учитывать. Плотность жидкости ρ=1000кг/
15.Определить давление р1 жидкости, которую необходимо подвести к гидроцилиндру, чтобы преодолеть усилие, направленное вдоль штока F=1кН. Диаметры: цилиндра D=50мм, штока d=25мм. Давление в бачке р0=50кПа, высота Н0=5м. Cилу трения не учитывать. Плотность жидкости ρ=1000кг/  .
.
Решение: Так как речь идет об определении давления, необходимо написать уравнение равновесия поршня. На поршень действуют три силы: две силы давления жидкости со стороны поршневой и штоковой полости и внешнее усилие F, приложенные к штоку. Уравнение равновесия запишем следующим образом:
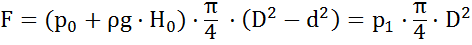 .
.
Из этого уравнения и определим искомую величину 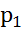

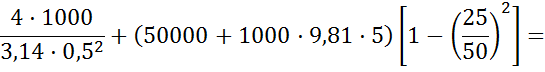

 16. Определить силу F на штоке золотника, если показание вакуумметра рвак=60кПа, избыточное давление р1=1МПа, высота Н=3м, диаметры поршней D=20мм и d=15мм, ρ=1000кг/
16. Определить силу F на штоке золотника, если показание вакуумметра рвак=60кПа, избыточное давление р1=1МПа, высота Н=3м, диаметры поршней D=20мм и d=15мм, ρ=1000кг/  .
.
Решение: Для определения силы F необходимо записать уравнение равновесия двухступенчатого поршня. На него действуют четыре силы: внешняя сила, приложенная к штоку, силы избыточного давления ρ1, приложенные к большой и малой ступеням поршня и сила, приложенная к малой ступени справа. Итак, уравнение равновесия:
 ,
,
откуда:
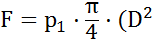 -
-  =
=

 =
=
= 132775-5,4 = 132Н.
 17. Определить давление р необходимое для удержания цилиндром Ц нагрузки F=70кН. Противодавление в полости 2 равно р2=0,3МПа, давление в полости 3 равно атмосферному. Размеры: Dц=80 мм, Dш=70мм, d1=50мм.
17. Определить давление р необходимое для удержания цилиндром Ц нагрузки F=70кН. Противодавление в полости 2 равно р2=0,3МПа, давление в полости 3 равно атмосферному. Размеры: Dц=80 мм, Dш=70мм, d1=50мм.
Решение: Чтобы определить давление р1, необходимо записать уравнение равновесия цилиндра, на который действуют две силы давления жидкости слева и справа и внешняя нагрузка F.
Слева действует сила  :
:
 -
- 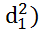 ,
,
где  -
-  - площадь кольцевой поверхности, на которую действует давление
- площадь кольцевой поверхности, на которую действует давление  Сила давление жидкости, действующая на цилиндр справа, по аналогии с предыдущем запишется следующим образом:
Сила давление жидкости, действующая на цилиндр справа, по аналогии с предыдущем запишется следующим образом:

Уравнение равновесия цилиндра в развернутом виде будет выглядеть так:

Запишем полученное выражение относительно искомой величины и определим ее численное значение

 +
+ 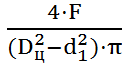 =
=
 +
+ 

 18. Определить силу, действующую на каждую из четырех стенок сосуда, имеющего форму перевернутой правильной пирамиды, если рм=0,5МПа, Н=4м, h=1,2м; каждая сторона основания пирамиды b=0,8м. Плотность жидкости ρ=800кг/
18. Определить силу, действующую на каждую из четырех стенок сосуда, имеющего форму перевернутой правильной пирамиды, если рм=0,5МПа, Н=4м, h=1,2м; каждая сторона основания пирамиды b=0,8м. Плотность жидкости ρ=800кг/  .
.
Решение: Сила, действующая на каждую из четырех стенок сосуда, равна произведению давления в центре тяжести стенки на ее площадь, т.е.
F = 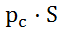 .
.
Давление в центре тяжести стенки складывается из манометрического ( на свободной поверхности жидкости) и весового давлений

Для равнобедренного треугольника, каковым являются боковые стенки правильной пирамиды, центр тяжести расположен на расстоянии 1/3 от основания. Площадь стенки определяется как половина произведения основания b на высоту стенки. Высота стенки выражается через высоту пирамиды и по теореме Пифагора будет равна
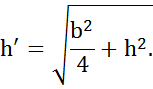
С учетом полученных выражений, формулу для определения силы F можно записать в следующем виде:

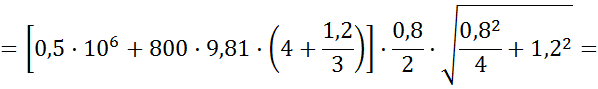

 19. Определить минимальное значение силы F, приложенной к штоку, под действием которой начнется движение поршня диаметром D=80мм, если сила пружины, прижимающая клапан к седлу, равна F=100Н, а давление жидкости
19. Определить минимальное значение силы F, приложенной к штоку, под действием которой начнется движение поршня диаметром D=80мм, если сила пружины, прижимающая клапан к седлу, равна F=100Н, а давление жидкости  . Диаметр входного отверстия клапана
. Диаметр входного отверстия клапана  =10мм ,диаметр штока
=10мм ,диаметр штока  =40мм, давление жидкости в штоковой полости гидроцилиндра р1=1МПа.
=40мм, давление жидкости в штоковой полости гидроцилиндра р1=1МПа.
Решение: Во всех задачах, где необходимо определить силу или давление, нужно записывать уравнение равновесия тела, о котором идет речь в задаче.
В данной задаче необходимо определить силу F, приложенную к штоку. Так как шток и поршень представляю собой единичное целое, нужно записать уравнение равновесия поршня и из него выразить искомую силу F. В классическом варианте на поршень гидроцилиндра всегда действуют три силы: сила давления рабочей жидкости слева и справа и внешняя сила, приложенная к штоку ( в данном случае искомая).
Сила давления жидкости слева от поршня (со стороны поршневой полости):

Сила давления жидкости справа от поршня (со стороны штоковой полости)
 -
- 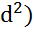 .
.
Таким образом, уравнение равновесия поршня:
 , или
, или 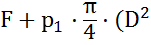 -
-  = 0,
= 0,
 -
-  -
- 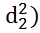 .
.
Из последнего уравнения видно, что в правой части есть неизвестная величина - давление в поршневой полости гидроцилиндра - pп.
Чтобы определить численное значение этого давления необходимо записать уравнение равновесия клапана. В силу того, что жидкость несжимаема, поршень не начнет перемещаться влево до тех пор, пока не откроется клапан. В момент открытия клапана на него, так же как и на поршень, действуют три силы: две силы давления жидкости и сила пружины F0.
Уравнение равновесия клапана, таким образом, запишется так:

откуда искомая величина:
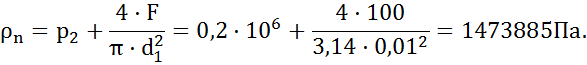
Сила, приложенная к штоку поршня:
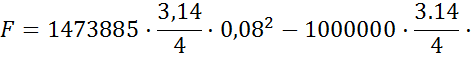

 20. Для обеспечения обратного хода гидроцилиндра его полость 1 заполнена воздухом под начальным давлением р1. Найти размер Ɩ, определяющий положение стопорного кольца 2, которое ограничивает ход штока. Размеры цилиндра:
20. Для обеспечения обратного хода гидроцилиндра его полость 1 заполнена воздухом под начальным давлением р1. Найти размер Ɩ, определяющий положение стопорного кольца 2, которое ограничивает ход штока. Размеры цилиндра: 


 Сила трения поршня и штока 400Н; давление слива
Сила трения поршня и штока 400Н; давление слива  2=0,3МПа; давление воздуха в начале обратного хода
2=0,3МПа; давление воздуха в начале обратного хода  =2МПа. Процесс расширения и сжатия воздуха принять изотермическим.
=2МПа. Процесс расширения и сжатия воздуха принять изотермическим.
Решение: Kлючом к решению этой задачи служит последнее предложение «Процесс расширения и сжатия воздуха принять изометрическим». Это означает, что для решения задачи нужно записать уравнение изотермы, т. е.
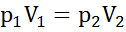 ,
,
где р1 и V1 - давление и объем воздуха в начале хода поршня; р2 и V2 - те же величины в конце хода поршня; Объемы V1 и V2 выразим через геометрические параметры цилиндра:
 .
.
Давление в начале хода поршня р1 =р1max. Давление в конце хода поршня, найдем из уравнения равновесия поршня, когда он остановится. На поршень действуют три силы: сила давления рабочей жидкости со стороны поршневой полости, где давление слива  , сила давления жидкости и сила трения направлены в одну сторону, противоположную силе давления воздуха
, сила давления жидкости и сила трения направлены в одну сторону, противоположную силе давления воздуха

отсюда давление воздуха в конце хода:


Полученные значения внесем в исходное уравнение, сократив общий множитель 
 , получим
, получим
2 · Ɩ = 1,3 · (L + Ɩ) или 2 · Ɩ - 1,3 · Ɩ = 1,3 · L
или 0,7 · Ɩ = 1,3 · 400, Ɩ = 742мм.
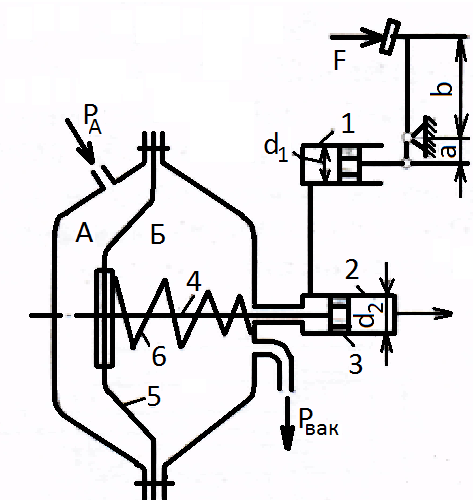 21. На рисунке показана принципиальная схема гидровакуумного усилителя гидропривода тормозов автомобиля. Давление жидкости, создаваемое в гидроцилиндре 1 благодаря нажатию на ножную педаль с силой F передается в левую полость тормозного гидроцилиндра 2. Помимо давления жидкости на поршень 3 в том же направлении действует сила вдоль штока 4, связанного с диафрагмой 5. Последняя отделяет полость А, сообщающуюся с атмосферой, от полости Б, где устанавливается вакуум благодаря соединению ее со всасывающим коллектором двигателя при нажатии на педаль. Пружина 6 при этом действует на диафрагму справа налево с силой Fпр. Определить давление жидкости, подаваемой из правой полости гидроцилиндра 2 к колесным тормозным цилиндрам. Принять: усилие педали F = 200Н; сила пружины Fпр = 20Н; давление в полости Б рвак = 0,06МПа; диаметры: диафрагмы: D = 100мм, гидроцилиндра 1 d1=25мм; гидроцилиндра 2 d2=20мм; отношение плеч b/a = 5. площадью сечения штока 4 пренебречь.
21. На рисунке показана принципиальная схема гидровакуумного усилителя гидропривода тормозов автомобиля. Давление жидкости, создаваемое в гидроцилиндре 1 благодаря нажатию на ножную педаль с силой F передается в левую полость тормозного гидроцилиндра 2. Помимо давления жидкости на поршень 3 в том же направлении действует сила вдоль штока 4, связанного с диафрагмой 5. Последняя отделяет полость А, сообщающуюся с атмосферой, от полости Б, где устанавливается вакуум благодаря соединению ее со всасывающим коллектором двигателя при нажатии на педаль. Пружина 6 при этом действует на диафрагму справа налево с силой Fпр. Определить давление жидкости, подаваемой из правой полости гидроцилиндра 2 к колесным тормозным цилиндрам. Принять: усилие педали F = 200Н; сила пружины Fпр = 20Н; давление в полости Б рвак = 0,06МПа; диаметры: диафрагмы: D = 100мм, гидроцилиндра 1 d1=25мм; гидроцилиндра 2 d2=20мм; отношение плеч b/a = 5. площадью сечения штока 4 пренебречь.
Решение: Для определения давления жидкости, подаваемой к колесным тормозным цилиндрам, необходимо записать уравнение равновесия поршня 3. На него действуют четыре силы: две силы давления жидкости слева и справа, сила пружины и сила давления воздуха на диафрагму. Последняя будет действовать и на поршень 3, т. к. он жестко связан с диафрагмой. Сила давления воздуха на диафрагму и сила давления тормозной жидкости слева стремятся переместить поршень 3 вправо. Этому перемещению препятствуют сила пружины и сила давления тормозной жидкости справа от поршня.

Запишем это уравнение относительно искомой величины р2:
 .
.
В правой части полученного уравнения неизвестно давление в левой полости гидроцилиндра 2-р1. Согласно закона Паскаля, такое давление будет и в полости верхнего гидроцилиндра. В верхнем гидроцилиндре это давление создается силой, действующей на шток поршня гидроцилиндра 1, которая в свою очередь, зависит от усилия на педали и соотношения плеч рычага в/а.
Таким образом, давление р1 можно выразить так:


Подставив численные значения всех величин в правой части уравнения для определения р2, получим его значение:
 .
.
 22. Из напорного бака вода течет по трубе диаметром d1=20мм, и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2=10мм. Избыточное давление воздуха в баке р0=0,18МПа; высота Н=1,6м. Пренебрегая потерями энергии, определить скорости течения воды в трубе ν1 и на выходе из насадка ν2.
22. Из напорного бака вода течет по трубе диаметром d1=20мм, и затем вытекает в атмосферу через насадок (брандспойт) с диаметром выходного отверстия d2=10мм. Избыточное давление воздуха в баке р0=0,18МПа; высота Н=1,6м. Пренебрегая потерями энергии, определить скорости течения воды в трубе ν1 и на выходе из насадка ν2.
Решение: Запишем уравнение Бернулли для сечений: 1 - 1- свободная поверхность воды в напорном баке; 2 - 2 - конец насадка; плоскость сравнения о-о - осевая линия трубы:

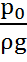 =
=  ,
,
из которого определим скорость истечения воды из насадка ν2


Скорость истечения по трубе найдем из уравнения расхода для потока жидкости

откуда
 =
=  .
.
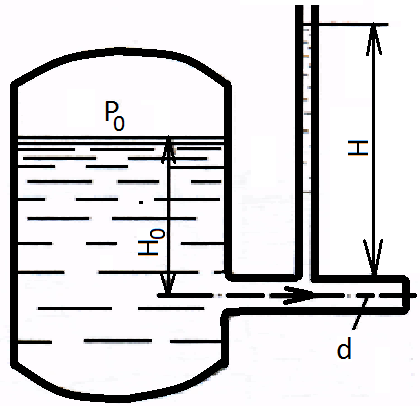 23.Определить расход керосина, вытекающего из бака по трубопроводу диаметром d=50мм, если избыточное давление воздуха в баке р0=16кПа, высота уровня Н0=1м, высота подъема керосина в пьезометре, открытом в атмосферу, Н=1,75м. Потерями энергии пренебречь. Плотность керосина ρ=800кг/
23.Определить расход керосина, вытекающего из бака по трубопроводу диаметром d=50мм, если избыточное давление воздуха в баке р0=16кПа, высота уровня Н0=1м, высота подъема керосина в пьезометре, открытом в атмосферу, Н=1,75м. Потерями энергии пренебречь. Плотность керосина ρ=800кг/  .
.
Решение: Эта задача, как и предыдущая решается с помощью уравнения Бернулли. В качестве сечений здесь принимаются: свободная поверхность керосина в баке - сечение 1-1 и место подсоединение к трубопроводу открытого пьезометра - сечение 2-2. Плоскость сравнения 0-0 - по осевой линии трубы.
Геометрический напор в первом сечении z=H0, пьезометрический:  ,
,
скоростной равен нулю, так как движения жидкости в первом сечении нет: уровень керосина в баке постоянный.
Для второго сечения геометрический напор z2=0, так как плоскость сравнения проходит через центр сечения 2-2, пьезометрический напор  =Н, скоростной напор во втором сечении
=Н, скоростной напор во втором сечении  запишем через расход и сечение трубопровода. Уравнение Бернулли в данном случае запишется следующим образом:
запишем через расход и сечение трубопровода. Уравнение Бернулли в данном случае запишется следующим образом:

Из исходного уравнения выразим искомую величину - расход керосина:



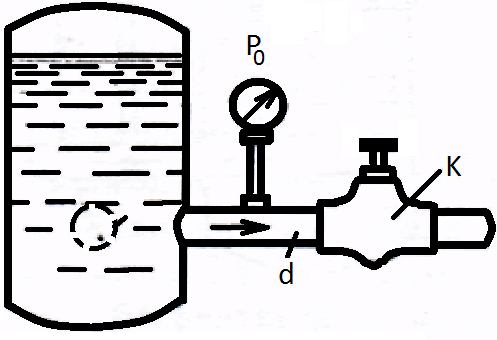 24. От бака, в котором с помощью насоса поддерживается постоянное давление жидкости, отходит трубопровод диаметром D=50мм. Между баком и краном К на трубопроводе установлен манометр. При закрытом положении крана р0=0,5МПа. Найти связь между расходом жидкости в трубопроводе Q и показанием манометра р при разных открытиях крана , приняв коэффициент сопротивления входного участка трубопровода (от бака до манометра) равным ζ=0,5. Плотность жидкости ρ=800кг/
24. От бака, в котором с помощью насоса поддерживается постоянное давление жидкости, отходит трубопровод диаметром D=50мм. Между баком и краном К на трубопроводе установлен манометр. При закрытом положении крана р0=0,5МПа. Найти связь между расходом жидкости в трубопроводе Q и показанием манометра р при разных открытиях крана , приняв коэффициент сопротивления входного участка трубопровода (от бака до манометра) равным ζ=0,5. Плотность жидкости ρ=800кг/  . Подсчитать расход жидкости при полном открытии крана, когда показание манометра равно р=0,485МПа.
. Подсчитать расход жидкости при полном открытии крана, когда показание манометра равно р=0,485МПа.
Решение: Запишем уравнение Бернулли для сечений: свободная поверхность жидкости в баке (1-1) и место подсоединение манометра к трубопроводу (2-2), плоскость сравнения по осевой линии трубы. Для первого сечения z1=0, т.к. в исходных данных его нет, пьезометрический напор при закрытом кране -  . Скоростной напор отсутствует (уровень жидкости в баке поддерживается постоянным). Для второго сечения геометрический напор z2=0, т.к. плоскость сравнения проходит через центр сечения; пьезометрический напор при открытом кране
. Скоростной напор отсутствует (уровень жидкости в баке поддерживается постоянным). Для второго сечения геометрический напор z2=0, т.к. плоскость сравнения проходит через центр сечения; пьезометрический напор при открытом кране  ; скоростной напор (скорость выражена через расход и сечение трубопровода)
; скоростной напор (скорость выражена через расход и сечение трубопровода)
 ;
;
потери напора на входном участке (по формуле Вейсбаха)
hм = 
 .
.
C учетом вышеизложенного уравнение Бернулли будет выглядеть следующим образом:
 =
=  +
+  ·
·  .
.
Из исходного уравнения можно выразить расход Q:


 .
.
Как видно из уравнения, при увеличении расхода показания манометра уменьшаются.
 25. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н=2м и постоянное давление р2=0,2МПа. Манометр, установленный на выходе из насоса на трубе диаметром
25. Насос нагнетает жидкость в напорный бак, где установились постоянный уровень на высоте Н=2м и постоянное давление р2=0,2МПа. Манометр, установленный на выходе из насоса на трубе диаметром
d=75мм. показывает р1=0,25МПа. Определить
расход жидкости Q, если диаметр искривленной трубы, подводящей жидкость к баку равен d=50мм, коэффициент сопротивления этой трубы принять равным ζ=0,5. Плотность жидкости ρ=800кг/  .
.
Решение:Для решения этой задачи нужно использовать уравнение Бернулли, записав его для двух сечений: сечение 1 - 1 - в месте подсоединения манометра к трубопроводу с диаметром  , сечение 2 - 2 - по свободной поверхности жидкости в баке, плоскость сравнения 0 - 0 - по осевой линии горизонтальной части трубы, т.к. относительно ее дано расстояние Н до свободной поверхности жидкости. Для выбранных сечений и плоскости сравнения уравнение Бернулли запишется следующим образом:
, сечение 2 - 2 - по свободной поверхности жидкости в баке, плоскость сравнения 0 - 0 - по осевой линии горизонтальной части трубы, т.к. относительно ее дано расстояние Н до свободной поверхности жидкости. Для выбранных сечений и плоскости сравнения уравнение Бернулли запишется следующим образом:

Последнее слагаемое в правой части уравнения, потери давления рп ,можно записать как

Скорости  1 и
1 и  2 можно выразить через расход и сечение труб, т.е.
2 можно выразить через расход и сечение труб, т.е.
 ;
; 
С учетом полученных выражений уравнение Бернулли будет содержать неизвестную величину Q.
 .
.
Перегруппировав члены уравнения и вынеся общие множители за скобки, получим следующее уравнение
 · (
· (  -
- 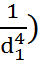 =
=  .
.
Из последнего уравнения получим



 26. Вода перетекает из напорного бака, где избыточное давление воздуха р=0,3МПа, в открытый резервуар по короткой трубе диаметром d=50мм, на которой установлен кран. Чему должен быть равен
26. Вода перетекает из напорного бака, где избыточное давление воздуха р=0,3МПа, в открытый резервуар по короткой трубе диаметром d=50мм, на которой установлен кран. Чему должен быть равен
коэффициент сопротивления крана для того, чтобы расход воды составлял Q=8,7 л/с? Высоты уровней  Учесть потерю напора на входе в трубу (ζ=0,5) и на выходе из трубы (внезапное расширение).
Учесть потерю напора на входе в трубу (ζ=0,5) и на выходе из трубы (внезапное расширение).
Решение: Уравнение Бернулли записывается для сечений, совпадающих со свободными поверхностями воды в напорном баке и резервуаре, и плоскость сравнения-осевая линия трубы. Здесь нужно отметить, что плоскость сравнения всегда горизонтальная плоскость и по условиям задачи относительно ее есть какие либо исходные данные (в данном случае - это уровни 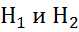 ).
).
Дата добавления: 2015-04-18; просмотров: 6451; Мы поможем в написании вашей работы!; Нарушение авторских прав |