Агроинженерия 3 страница

Уравнение Бернулли целесообразнее записать по избыточному давлению, т.е.

,

откуда - суммарные потери напора на местных сопротивлениях. Эти потери можно выразить, используя формулу Вейсбаха, как

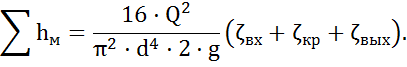
Приравняем правые части полученных выражений для суммарных местных потерь:

· .

Разделим обе части уравнения на

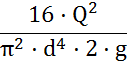
и коэффициенты перенесем в правую часть уравнения с обратным знаком, получим:

Пояснение: при внезапных расширениях, в данном случае , коэффициент местного сопротивления определяется по формуле Борда. Однако, при несоизмеримых размерах сечений бака и трубы его принимают равным единице (

27. Бензин сливается из цистерны по трубе диаметром d=50 мм, на которой установлен кран с коэффициентом сопротивления ζ=3. Определить расход бензина при и , если в верхней части цистерны имеет место вакуум h=73,5 мм рт. ст. Потерями на трение в трубе пренебречь. Плотность бензина ρ=750кг/м.

Решение: Для решения задачи используем уравнение Бернулли, записанное относительно двух сечений: сечение 1-1 - по свободной поверхности бензина в цистерне, сечение 2-2 - по свободной поверхности бензина в резервуаре. Плоскость сравнения целесообразно совместить со вторым сечением.
.

Абсолютное давление на поверхности бензина в цистерне запишем через исходные данные

Скорость в правой части выразим через расход и сечение трубы

υ = .

С учетом полученных выражений уравнение Бернулли запишем следующим образом:

· .

Последнее слагаемое в правой части умножаем на , переводя мм рт. ст. в м рт. ст. Последнее уравнение запишем относительно искомой величины Q и найдем ее численное значение

·

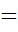
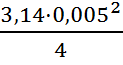= 1,9625·10^-3·

28. Вода перетекает из напорного бака А в резервуар Б через вентиль с коэффициентом сопротивления ζ=3 по трубе. Диаметры:

Считая режим течения турбулентным и пренебрегая

потерями на трение на длине, определить расход. Учесть потери напора при внезапных сужениях и расширениях. Высоты: Н₁=1м, Н₂=2м; избыточное давление в напорном баке Р₀=0,15МПа.

Решение: Запишем уравнение Бернулли относительно сечений: 1-1 - свободная поверхность воды в напорном баке, 2-2 - свободная поверхность воды в резервуаре и плоскости сравнения взятой по осевой линии трубы.

,

где - суммарные местные потери определяются по формуле Вейсбаха

·( ,

где - коэффициенты местных сопротивлений при внезапных сужениях и расширениях а также вентиля . Когда сечение трубы несоизмеримо мало с сечением бака или резервуара, = 0,5 а 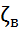· е = 1. Для труб разного сечения коэффициенты внезапного сужения и внезапного расширения определяются: первый по формуле Идельчика:

,

где площади сечения труб до и после сужения. Для круглых труб:

Второй - по формуле Борда:

,

где: - площади сечении до и после расширения труб. Выразив сечения через диаметры труб, последнее выражение можно записать следующим образом:

Подставим в исходное уравнение выражение для суммарных местных потерь напора и далее из него выразим искомую величину - расход Q.

и .

Заменив величины в правой части уравнения их численными значениями, определим расход.

29. По длинной трубе диаметром d = 50 мм протекает жидкость (v = 2 Ст; = 900 кг/ ). Определить расход жидкости и давление в сечении, где установлены пьезометр (h = 60 см) и трубка Пито (H = 80 см).

Решение: Давление в сечении определяется по показанию пьезометра :

Трубка Пито помимо пьезометрического учитывает еще и скоростной напор, т. е. ,

откуда

,

где - α коэффициент Кориолиса.

Прежде чем определить расход , необходимо установить режим течения с помощью критерия Рейнольдса

= .

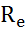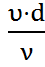Выражение для скорости получим из предыдущего уравнения:

υ_л = ;

;

Итак, при ламинарном режиме скорость составит 1,4 м/с, а при турбулентном 1,98 м/с. Подставим значение скоростей для определения числа Рейнольдса.

; ;

Вычисленные по уравнению числа Рейнольдса меньше его критического значения, следовательно, режим ламинарный и для определения расхода берем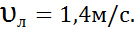

Таким образом, расход Q:

.

30. Выходное сечение жиклера карбюратора расположено выше уровня бензина в поплавковой камере на h = 5 мм, вакуум в диффузоре:

Пренебрегая потерями напора, найти расход бензина Q, если диаметр жиклера d=1мм. Плотность бензина р=680 кг/ .

Решение: По выбранным и указанным на схеме сечениям и плоскости сравнения запишем уравнение Бернулли:

.

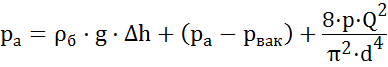Здесь ( 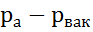) – абсолютное давление в устье жиклера. Третье слагаемое в правой части – скоростное давление, выражение через расход и сечение жиклера. Исключив в обеих частях уравнения, запишем его относительно неизвестный величин расхода Q:

= =

= 4,66 · 10^-6 м³/с 4,66 см³/с.

31. По трубопроводу диаметром d=12мм перекачивается масло индустриальное ИС-20 ( =890кг/м³) с температурой 30⁰С (ν=47мм²/с). Определить показания h ртутного дифференциального манометра, присоединенного к трубопроводу в двух точках, удаленных друг от друга на расстояние l=3м, если расход масла Q=0,3 л/с.

Решение: Так как трубопровод горизонтальный и на всей длине одинакового диаметра, то для сечений трубопровода в местах присоединения трубок дифманометра уравнение Бернулли можно записать следующим образом:

, или △ ,

где △р – потери давления в трубопроводе на длине Ɩ. Прежде чем определять потери давления, необходимо установить режим течения масла по трубопроводу с помощью критерия Рейнольдса:

Вычисленное по уравнению число Рейнольдса меньше критического, следовательно режим течения ламинарный. В этом случае для определения потерь давления в трубопроводе используется формула, известная, как закон Пуазейля:

Для того чтобы определить искомую величину h, необходимо записать основное уравнение гидростатики для точек В и С, находящихся на поверхности равного давления (поверхность раздела масла и ртути в левом колене дифманометра).

Давление в т. В: ;

Давление в т. С: .

Приравняем правые части полученных выражений :

.

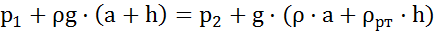Запишем разность давлений ( ):

,

откуда искомая величина h будет равна :

.

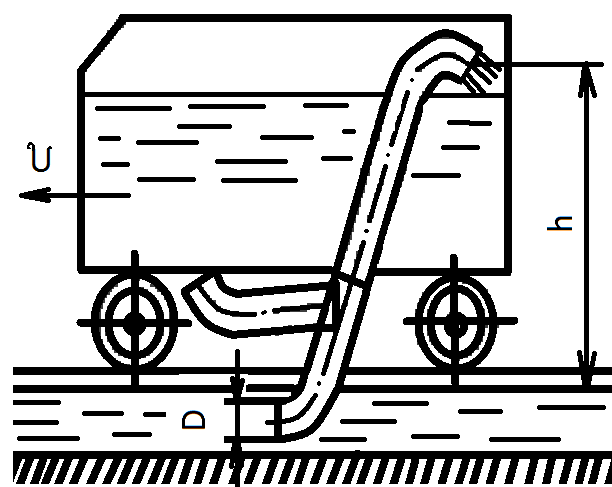32. Для заполнения водой паровозного тендера на ходу поезда, в специально устроенный между рельсами лоток с водой опускается труба приемного устройства диаметром D=200мм так, что входное сечение трубы располагается навстречу потоку. Суммарный коэффициент потерь в приемном устройстве, отнесенный к средней скорости в трубе, равен ζ=2, а высота подъема воды h=3м. Определить: 1. время, необходимое для заполнения тендера ёмкостью V=10м³ при скорости поезда υ=36км/ч; 2. при какой наименьшей скорости поезда это устройство перестанет работать.

Решение:1. Время необходимое для заполнения тендера водой:

.

Чтобы определить неизвестную величину - расход Q, необходимо записать уравнение Бернулли, выразив скоростной напор через расход и сечение трубы, для сечений: 1 - начало трубы, 2 - конец трубы, плоскость сравнения - по осевой линии трубы в первом сечении:

= h + + ,

или .

Из этого уравнения выразим расход и определим его численную величину:

= м³/с. 116л/с.

Здесь

Время заполнения тендера водой:

2 Приемное устройство перестанет работать, когда расход станет равным нулю и уравнение Бернулли в этом случае запишется следующим образом :

откуда

.

33. Для определения потерь давления на фильтре установлены манометры, как показано на рисунке. При пропускании через фильтр жидкости, расход которой Q=1л/с; давления: Определить, чему равна потеря давления в фильтре , если известно: . Указание: Потерей давления на участках от мест установки манометров до фильтра пренебречь, принять

Решение: Задача решается с помощью уравнения Бернулли для сечений в местах установки манометров на трубопроводе и плоскости сравнения, совпадающей с осевой линией трубопровода:

,

откуда

.

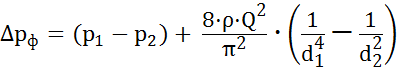Подставляя численные значения величин в правой части уравнения, определим потери давления на фильтре:

.

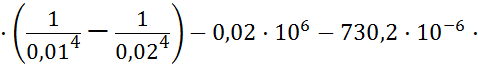
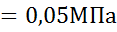34. Определить скорость перемещения поршня вниз, если к его штоку приложена сила F=10кН. Поршень диаметром D=50мм имеет пять отверстий диаметром d₀=2мм каждое. Отверстия рассматриваются как внешние цилиндрические насадки с коэффициентом расхода µ=0,82; =900кг/м³.

Решение: Из уравнения расхода скорость поршня определится как

= = .

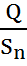Неизвестную величину расхода запишем по формуле для определения расхода через отверстие:

.

Перепад давления на отверстиях обусловлен внешней силой F:

.

Заменяя Q и △р их выражениями , определим скорость перемещения поршня:

35. Oпределить направление истечения жидкости ( = _вод) через отверстие =5мм и расход, если разность уравнений Н=2 м, показание вакуумметра соответствует 147мм рт. ст., показание манометра =0,25МПа, коэффициент расход µ=0,62.

Решение: Предположим, что направление истечения жидкости через отверстие справа-налево и запишем для этого случая расход через отверстие :

Q =

=

.

В даном случае - абсолютное давление в правом отсеке:

;

абсолютное давление в левом отсеке:

.

И, таким образом, заменив и их значениями, получим что

Что и было записано в численных величинах под корнем. Так как выражение под корнем имеет знак (+), следовательно, направление истечения выбрано верно. В противном случае выражение под корнем имело бы знак (-).

36. При исследовании истечения через круглое отверстие диаметром =10мм получено: диаметр струи ; напор Н=2м; время наполнения объема V=10л; t=32,8 с. Определить коэффициенты сжатия ε, скорости φ, расхода µ и сопротивления ξ. Распределение скоростей по сечению струи считать равномерным.

Решение: По исходным данным сразу можно определить коэффициент сжатия:

ε = 0,64.

По расходу и диаметру струи можно определить скорость струи:

.

Коэффициент скорости представляет собой отношение скорости истечения реальной жидкости к скорости истечения идеальной жидкости, т.е. к жидкости, истекающей без потерь.

Коэффициент скорости:

= = .

По значениям коэффициентов сжатия и скорости определим коэффициент расхода:

µ = · ε = 0,97 · 0,64 = 0,62.

Так как распределение скоростей по сечению струи равномерное, следовательно, режим течения турбулентный, для которого α=1.

Коэффициент скорости определяется по формуле:

= ; или в данном случае = 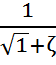, откуда

ζ =

37. Hа рисунке изображена схема устройства, известного под названием «Геронов фонтан». Трубы А и Б заполнены водой, а труба В – воздухом. Объяснить принцип действия и определить скорость истечения воды из насадка (сопла) этого фонтана, если размеры Н₁=24м; Н₂=4м; Н₃=0,4м. Потерями напора в системе и весом воздуха в трубе В пренебречь.

Решение: «Геронов фонтан» работает следующим образом. Вода из верхнего бака по трубе А сливается в нижней герметично закрытый , сжимая тем самым и вытесняя по трубе В воздух в средний герметичный бак. Под давлением сжатого в среднем баке воздуха вода из него по трубе Б с большой скоростью поднимается вверх, образуя фонтан. Скорость истечения воды из насадка на трубе Б определяется по известной формуле:

υ =

= .

В данном случае величины взяты со знаком (-), т.к. располагаемый геометрический напор в виде , будет расходоваться на подъем воды на высоту и на трансформацию в скоростной напор.

38. Вода по трубе Т подается в резервуар А, откуда через сопло диаметром =9мм перетекает в резервуар Б. далее через внешний цилиндрический насадок =10мм вода попадает в резервуар В и, наконец вытекает в атмосферу через внешний цилиндрический насадок =6мм. При этом Н=1,1м; b=25мм. Определить расход воды через систему и перепады уровней . Коэффициенты истечения принять: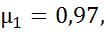

Решение: Так как вода перетекает из одного резервуара в другой при установившихся уровнях в них, то расходы через насадки будут одинаковы , т.е.

.

Первые два насадка подтоплены и в качестве действующих напоров здесь будут выступать разности уровней в резервуарах. С учетом этого запишем расходы через каждый насадок:

;

;

.

В последнем уравнении все данные в правой части известны и можно определить расход воды через систему.

.

По известному расходу системы из первых двух уравнений найдем разности .