Агроинженерия 4 страница

Разности уровней можно определить и по другому, приравнивая последовательно правые части первого и третьего, второго и третьего уравнений.

;

.

Сократив общие множители и возведя в квадрат оба уравнения, запишем их относительно искомых величин

;

.

Подставим численные значения величин в правой части уравнений, найдем .

.

39. Жидкость с плотностью =850кг/ подается от насоса в гидроцилиндр, а затем через отверстие в поршне площадью =5 и гидродроссель, Д в бак (р_б, = 0).

1. Определить, при какой площади проходного сечения дросселя Д поршень будет находиться в неподвижном равновесии под действием силы F=3000H, если диаметр поршня D=100мм, диаметр штока D_ш=80мм, коэффициент расхода отверстия в поршне =0,8, коэффициент расхода дросселя , давление насоса

2. Определить площадь проходного сечения дросселя Д, при которой поршень будет перемещаться со скоростью υ=1см/с вправо.

Решение:1. При неподвижном поршне расходы через отверстие и дроссель будут одинаковы

.

Запишем выражения для и , а затем приравняв правые части этих выражений , найдем искомую величину -сечение дросселя .

,

откуда

.

В правой части уравнения неизвестна величина давления жидкости в поршневой полости гидроцилиндра . Для того чтобы определить это давление необходимо записать уравнение равновесия поршня, на который действуют две силы давления жидкости и внешняя сила F, приложенная к штоку поршня ( классический вариант нагружения поршня):

,

откуда

=

Подставив полученное значение в формулу для определения , найдем его величину:

.

1. Когда поршень будет перемещаться вправо со скоростью 1см/с, расход через отверстие будет больше чем расход через дроссель и уравнение расходов можно представить как

= υ или .

Запишем расходы через отверстие и дроссель и из полученного уравнения выразим искомую величину

= ,

откуда

=

Пояснение: В подкоренном выражении в числителе плотность измерена в кг/ поэтому появился переводной коэффициент . Аналогичным образом в знаменателе в размерности давления вместо м, записывается мм, т.е. 1МПа=1Па/мм²=1кг·м/с²·мм² = 10³кг·мм/(с²·мм²)и появился переводной коэффициент

40. Считая жидкость

несжимаемой, определить скорость движения поршня под действием силы F=10кН на штоке, диаметр поршня D=80 мм, диаметр штока d=30мм, проходное сечение дросселя =2мм², его коэффициент расхода µ=0,75, избыточное давление слива =0, плотность рабочей жидкости =900кг/ .

Решение: Для решения этой задачи прежде всего необходимо записать уравнение расходов. Из схемы видно, что расход жидкости из поршневой полости равен сумме расходов через дроссель и в штоковую полость , т. е.

Расходы поршневой и штоковой полости можно выразить через скорость поршня и сечение штока в поршневой и штоковой полостях и исходное уравнение можно представить следующим образом:

,

или

.

Из последнего уравнения выражаем скорость поршня

.

Для определения неизвестной в правой части величины расхода через дроссель запишем известную формулу

.

Перепад давления на дросселе △р равен давлению в поршневой и штоковой полости , т. е. △р=р_n=р_шт, т. к. поршневая и штоковая полости и дроссель соединены трубопроводом, потери в котором равны нулю. Для определения давления нужно записать уравнение равномерного движения поршня т. е. сумму всех сил, действующих на него, приравнять к нулю. На поршень действуют две силы давления жидкости со стороны поршневой и штоковой полости и внешняя F, приложенная к штоку.

= F.

Решая это уравнение относительно искомой величины р, находим что давление равно:

По найденному давлению определим расход жидкости через дроссель

Скорость поршня:

41. Определить, пренебрегая потерями напора, начальную скорость истечения жидкости из сосуда, заполненного слоями воды и масла (относительная плотность δ=0,8) одинаковой высоты h=1м. Сравнить полученный результат с начальной скоростью истечения при заполнении сосуда только водой или только маслом до уровня 2h.

Решение: Начальная скорость истечения воды и масла определяется по формуле:

При заполнение сосуда только водой:

При заполнение сосуда только маслом

Скорость истечения получается наименьшей при заполнении сосуда только маслом в силу меньшей его, по сравнению с водой, плотности. В силу этого меньшим будет и действующий напор.

42. Вода по трубе 1 подается в открытый бак и вытекает по трубе 2. Во избежание переливания воды через край бака устроена вертикальная сливная труба 3 диаметром d=50мм. Определить необходимую длину L трубы 3 из условия, что при =10л/с и перекрытой трубе 2 ( =0) вода не переливалась через край бака. Режим течения считать турбулентным. Принять следующие значения коэффициентов сопротивления: на входе в трубу =0,5; в колене =0,5; на трение по длине трубы =0,03; a=0.

Решение: Эту задачу можно решить, используя уравнение Бернулли для двух сечений: свободная поверхность трубы - сечение 1-1 (начало потока) и конец трубы - сечение 2-2 (конец потока). Плоскость сравнения целесообразно совместить со вторым сечением. Уравнение запишем по избыточному давлению, которое в данном случае отсутствует (истечение происходит из открытого бака в атмосферу).геометрический напор для сечения 1-1 равен длине сливной трубы 2 (геометрический напор - это расстояние от центра сечения до плоскости сравнения); скоростной напор отсутствует: уровнень воды в баке постоянный. Во втором сечении будет скоростной напор и потери напора (линейные и местные). Скоростной напор:

или .

Потери напора:

или

Таким образом, уравнение Бернулли можно записать в следующем виде:

Полученное уравнение необходимо решить относительно искомой величины - длины сливной трубы L. Прежде всего обе части уравнения поделим на и перенесём в одну часть уравнения члены, содержащие неизвестную величину, а не содержащие - в другую.

L· .

Приведем слагаемые в левой части уравнения к общему знаменателю и умножив на него обе части уравнения, вынесем в левой части общий множитель за скобки:

,

откуда

L = =

= =

=

43. Определить силу F, которую нужно приложить к поршню насоса диаметром D=65мм, чтобы подавать в напорный бак жидкость с постоянным расходом Q=2,5л/с. Высота подъема жидкости в установке =10м, избыточное давление в напорном баке =0,15МПа. Размеры трубопровода Ɩ=60м, d=30мм; его шероховатость △=0,03мм. Коэффициент сопротивления вентиля на трубопроводе ζ=5,5, потери напора на плавных поворотах трубопровода не учитывать. Задачу решить для случая подачи в бак бензина ( =765кг/м³, v=0,4сСт) и машинного масла ( =930кг/м³, v=20сСт). Трением поршня в цилиндре пренебречь.

Решение: При равномерном движении поршня сила F, приложенная к поршню слева, должна быть равна силе давления жидкости справа т. е.

F = p · · .

Чтобы определить давление р справа от поршня нужно записать уравнение Бернулли для сечений: 1-1 - сразу за поршнем справа, 2-2 свободная поверхность жидкости в напорном баке; плоскость сравнения - осевая линия насоса. Это же уравнение можно записать, понимая энергетический смысл процесса. При подаче в бак жидкости с расходом Q, энергия жидкости, сообщаемая ей насосом в виде давления р, расходуется на высоту (в размерности давления эта величина равна · g · ), на преодоление противодавления и на преодоление сопротивлений в трубопроводе. Таким образом, уравнение Бернулли в размерности давления запишем следующим образом:

р = · g · + .

Чтобы определить потери давления необходимо установить режим течения жидкости в трубопроводе с помощью критерия Рейнольдса:

.

1. для бензина:

= 265393.

2. для масла:

.

Вычисленные по уравнению числа Рейнольдса значительно больше критического . Следовательно, режим течения бензина и масла турбулентный и для определения потерь в трубопроводе используем формулу Вейсбаха-Дарси, причем скорость выражаем через расход и сечение трубопровода:

.

1. Неизвестный коэффициент гидравлического трения для бензина определим по формуле Шифринсона (область гидравлически шероховатых труб на графике Никурадзе):

= 0,11· .

Потери давления при течении по трубопроводу бензина:

Давление перед поршнем насоса:

р = 765·9,81·10+150000+217912=442958Па=443кПа.

Сила, приложенная к поршню насоса:

F = 443 · · .

2. Для масла коэффициент λ определяем по формуле Блазиуса, так как число Рейнольдса меньше (область гидравлчески гладких труб на графике Никурадзе):

λ = .

Потери давления:

Δр =

Давление, создаваемое насосом:

р = 930 · 9,81 · 10 + 150000 + 462869 = 704102Па = 704кПа.

Сила, приложенная к поршню:

F = 704102 · = 2335Н = 2,34кН.

44. Смазочное масло подводится к подшипникам коленчатого вала по системе трубок, состоящей из пяти одинаковых участков , каждый длиной Ɩ=500мм. Сколько смазки нужно подать к узлу А системы, чтобы каждый подшипник получил ее не менее 8 /с? Как изменится потребное количество смазки, если участок АВ заменить трубой диаметром D=8мм? Давление на выходе из трубок в подшипники считать одинаковыми, местными потерями и скоростными напорами пренебречь.

Решение: Так как давление на выходе из трубок в подшипники одинаково, то данный разветвленный трубопровод можно считать, как при параллельном соединении труб, т. е. расходы по участкам складываются а потери напора на участках одинаковы, т. е

Q = ; .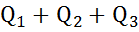

Условимся нумеровать подшипники слева направо и длины участков будем считать от узловой т. А до соответствующего подшипника, т.е. для первого подшипника она будет равна 3Ɩ, для второго 2Ɩ, и для третьего – lƖ. Прежде чем определять потери напора на участках, необходимо установить режим течения масла в трубках с помощью критерия Рейнольдса

.

Вычисленное по уравнению число Рейнольдса меньше критического, следовательно, режим течения ламинарный и для определения потерь напора используем формулу Пуазейля. На первом участке на длине l расход масла будет равен сумме расходов первого и второго подшипников и на длине 2l расход равен расходу первого подшипника и потери напора, таким образом, можно записать следующим образом:

.

Для второго участка на длине l расход равен сумме расходов первого и второго подшипников и на длине Ɩ - расходу второго подшипника т. е.

.

Для третьего участка:

.

Приравнивая последовательно правые части полученных выражений, выразим расходы на втором и третьем участках через расход на первом участке, сократив при этом общие множители.

Итак:

или

или .

или ,

или = 5 .

Подставим значения расходов в исходное уравнение, получим

Q = =8 + 2 · 8 + 5 · 8 = 64 см³/с.

Если диаметр магистрального участка трубопровода увеличен в два раза, то уравнения для определения потерь напора на участках запишутся следующим образом:

h₁ = · ;

h₂ = · ; h₁ = · Q₃.

Используя те же приемы, что и в первом случае запишем, что

и

+ 17/16 .

Подставив полученные выражения для и получим:

Q =

см³/с.

Цифра 16 получается потому, что диаметр

d^ˡ = 2 · d, .

45. При испытании насоса получены следующие данные: избыточное давление на выходе из насоса =0,35МПа; вакуум перед входом в насос =294мм рт. ст, подача Q=6,5л/с; вращающий момент на валу насоса М=41Н·м; частота вращения вала насоса n=800об/мин. Определить мощность, развиваемую насосом, потребляемую мощность и КПД насоса. Диаметры всасывающего и напорного трубопроводов считать одинаковыми.

Решение: Записываем выражение для определения КПД насоса

Η = ,

где -полезная мощность насоса; −потребляемая мощность.

Полезная мощность насоса определяется как произведение давления насоса на его подачу

.

Давление насоса равно разности абсолютных давлений в нагнетательном и всасывающем трубопроводах.

.

Вакуумметрическое давление:

.

Подставляя полученные выражения для , получим:

.

Мощность потребляемая:

N = M · ω = M · =

.

КПД насоса:

η =

46. Центробежный насос системы охлаждения двигателя имеет рабочее колесо диаметром =200мм, с семью радиальными лопатками, диаметр окружности входа =100мм. Какую частоту вращения нужно сообщить валу этого насоса при работе на воде для получения давления насоса р=0,2МПа? Гидравлический КПД насоса принять равным η_г=0,7.

Решение: Вначале запишем формулу, из которой можно выразить искомую частоту вращения вала насоса:

или ,

откуда n = .

В правой части уравнения неизвестна окружная скорость . Необходимо написать формулу, в которую входила бы эта величина - это формула для определения теоретического напора насоса при схеме бесконечного числа лопаток:

= ).

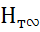Так как угол β=90, и второе слагаемое в скобках тоже равно нулю и, таким образом,

откуда .

С другой стороны, действительный напор насоса можно представить как:

Н = ,

а теоретический при схеме бесконечного числа лопаток