Итерационный метод решения обратной кинематической задачи (алгоритм Ньютона). Сущность метода. Управление скоростью сходимости метода.

Среди итерационных алгоритмов наиболее прост и удобен алгоритм Ньютона. Воспользуемся алгоритмом Ньютона второго порядка (алгоритм имеет порядок n, если в нем используются производные функций до (n – 1)-го порядка включительно). Этот алгоритм является компромиссным между двумя важными требованиями к итерационному процессу решения ОЗК в реальном масштабе времени: быстротой сходимости и объемом вычислений. В одномерном случае при решении уравнений f (x) = 0 алгоритм Ньютона второго порядка имеет вид

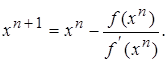(2.22)

Из (2.22) видно, что для успешного решения уравнения f(x) = 0 требуется некоторое «достаточно хорошее» начальное приближение x₀, такое, чтобы в области x_N – x₀, где x_N – корень уравнения f(x) = 0, функция f(x) менялась монотонно ( (x) ¹ 0), т. е. x_N – x₀ должно быть (при произвольной f(x)) достаточно мало.

Опыт показывает, что вдоль программной траектории 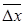настолько мало, что вторым слагаемым в (2.21) можно пренебречь, считая первое слагаемое главной частью приращения 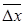. Физически малость вектора 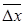в (2.21) означает малость его в сравнении с размерами рабочей зоны ИМ X.

Рассмотрим алгоритм Ньютона для решения ОЗК. Пусть 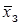- заданное значение технологических координат; 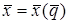- ПЗК; - ошибка при итерации. Найдем корни 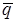системы уравнений = 0. По условию . Пусть 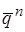- некоторое приближение к корням; 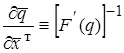. Получим следующий алгоритм:

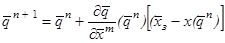. (2.23)

Данный способ построения алгоритма Ньютона имеет следующие технические недостатки (при максимально возможной динамической точности решения ОЗК):

- сложность переключения на управление положением в обобщенных координатах;

- интервал дискретизации при решении ОЗК должен быть мал и равен интервалу дискретизации при расчете системы управления скоростью ИМ.