Задача управления ИМ ставится следующим образом.

Дана математическая модель ИМ в виде (2.47). Требуется построить такое управление , чтобы вид переходного процесса системы управления соответствовал заданному критерию оптимальности.

26. Построение дуги окружности: подготовительные и диагностические операции. Алгоритм построения дуги окружности.

Планирование и построение дуги окружности выполним в полярных координатах, так как при этом дуга окружности будет прямой линией. Для выполнения операций в полярных координатах следует считать в них граничные условия, заданные в декартовых координатах, нормировать угол дуги в пределах, например, от 0 до 2p. Уравнение дуги окружности – в общем случае сумма трех векторов (рис. 2.11):

, (2.5)

где - вектор параллельного переноса относительной системы координат, связанной с вектором начальной точки дуги ; - вектор смещения центра окружности, которой принадлежит дуга в относительной системе координат; - радиус-вектор рассматриваемой дуги; – вектор точки, перемещающейся по дуге, выраженный в абсолютной системе координат (например, в системе координат станка).

На рис. 2.11 представлена плоскость X0Y. Совершенно аналогичное построение можно выполнить в двух других плоскостях. Предполагается, что для построения дуги в данном случае заданы начальный и конечный векторы и вектор (своими проекциями I и J на оси X и Y соответственно):

Параметрические уравнения окружности, как следует из рис. 2.11, имеют вид:

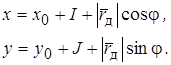. (2.6)

На рис. 2.11 выбрано направление обхода дуги «по часовой стрелке», тогда

x = x₀, если j = p + 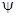= j₀. Найдем j₀, для чего определим :

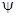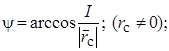если J < 0, то 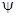: = 2p - 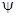. Для нормировки угла

j₀ в пределах 0 ¸ 2p следует положить: если j₀ > 2p, то j₀: = j₀ - 2p.

Аналогично поступим с определением угла j_к:

Если y_K – y_С < 0, то j_K: = 2p - j_K. Таким образом, при решении уравнений (2.6) j₀ £ j < j_K и j₀, j_K и j Î [0, 2p).

Рассмотрим этап планирования дуги окружности:

1. Вычисление радиуса дуги .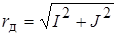

Если r_Д > r_max и , то дугa не строится (r_minследует полагать не менее чем 10 дискрет измерительной системы ИМ, r_max зависит от размеров рабочей зоны ИМ).

2. Расчет приращения угла поворота радиус-вектора за один такт дискретизации:

Dj = ± ,

где v – контурная скорость (постоянная для всей дуги); Т – длительность такта дискретизации; k – коэффициент выбора единиц измерений; «+» – означает направление обхода дуги «против часовой стрелки».

3. Проверка условия, что вектор конечной точки лежит на дуге окружности с точностью до радиальной составляющей методической погрешности. Должно выполняться неравенство:

в противном случае дуга не строится.

4. Алгоритм расчета функции arccos имеет ограничения, которые следует учесть:

если > 0,999… или < – 0,999…, то следует положить:

= ± 0,999… (для формата двойной вещественной точности число «девяток» равно тринадцати). Аналогично следует анализировать .

5. Формирование начального значения угла j и установка признака разрешения расчета дуги окружности:

j: = j₀.

Рассмотрим этап исполнения дуги окружности.

1. Признак разрешения расчета дуги установлен?

Нет, выход; да, перейти на п. 2 .

2. Анализ конца дуги:

½j - j_к½ £ ½Dj½? да, j: = j_к,

сбросить признак разрешения расчета дуги, на п. 4;

нет, j: = j + Dj, на п. 3.

3. Выполнение нормировки угла j:

j < 0? да? j: = j + 2p, на п. 4;

j > 2p? да, j: = j - 2p, на п. 4;

нет, на п. 4.

4. Расчет точки, лежащей на дуге:

Этот алгоритм также не имеет циклов, подобно алгоритму построения прямолинейной траектории.

28.Задача вывода пространственного механизма в исходное положение (задача калибровки): назначение, общий алгоритм.

Задачу вывода механизма в исходное положение иногда называют задачей калибровки координат ИМ, так как результатом ее решения является определение начала отсчета той или иной системы координат и масштаба по координатам. Решение задачи калибровки существенно зависит от технических особенностей измерительной системы ИМ. Так, в случае энергонезависимых датчиков абсолютного отсчета калибровки вообще не требуется, так как начало отсчета и масштаб определены установкой датчиков. Для измерительных систем с двумя датчиками (датчики грубого и точного отсчетов) калибровка локализована в пределах одной дискреты датчика грубого отсчета. Для измерительной системы с двухканальными датчиками (точный отсчет – линейная шкала, грубый отсчет – нелинейная шкала) калибровка также осуществляется в пределах одной дискреты нелинейной шкалы. Рассмотрим наиболее распространенный вариант измерительной системы – с датчиками относительного отсчета. Для этого определим разметку обобщенных и технологических координат ИМ.

Для технологических координат рабочая зона X ограничена программными упорами (рис. 2.21), используемыми в задаче контроля границ рабочей зоны. Для обобщенных координат наряду с программными имеются механические упоры и совокупность конечных выключателей для функций калибровки и контроля (рис. 2.22). Программные упоры используются в задаче контроля границ рабочей зоны.

Механические упоры предохраняют ИМ от возможного разрушения. Датчики верхней и нижней границ рабочей зоны определяют предельный физический диапазон, в котором могут устанавливаться программные упоры, а также служат целям выхода ИМ в исходное положение. Датчики выхода в исходное положение и нуль-метки позволяют осуществить калибровку с предельной точностью, доступной измерительной системе ИМ.

Алгоритм задачи вывода ИМ в исходное положение состоит в следующем:

1. Предполагается, что вектор положения находится в пределах рабочей зоны Q (нормальный режим) (рис. 2.23) и начинается движение к нижней границе со скоростью v₁ под управлением регулятора скорости
(v₁ >> v₂ > v₃).

2. При достижении нижней границы скорость изменяется до v₂ и ИМ двигается до срабатывания датчика приближенного выхода в исходное положение.

3. При достижении исходного положения требуется точное позиционирование (с точностью до одной дискреты измерительной системы), осуществляемое со скоростью v₃ до прихода нуль-метки.

4. При достижении нуль-метки проводятся подготовительные операции, связанные с регистрацией начала обобщенных координат ИМ.

Данный алгоритм должен производить обработку как всех координат ИМ одновременно, так и любой из них по выбору.