Алгоритмы разгона и торможения. Сравнительная оценка алгоритмов. Примеры.

Алгоритмы разгона и торможения пространственного механизма (ПМ) имеют ряд особенностей, отличающих их от аналогичных алгоритмов для автоматизированных электро- и гидроприводов.

Эти особенности следующие.

1. Совместное управление координатами (осями) ПМ. Оно придаёт указанным алгоритмам векторный характер, так что возникает необходимость в специфических операциях планирования движений.

2. Вид траектории программного управления. Он влияет на выбор алгоритмов разгона и торможения ПМ.

3. Кадровая структура и семантика управляющей программы (УП) для ПМ. Она накладывает ряд условий на применение алгоритмов разгона и торможения.

Писать в конце:

Алгоритмы разгона и торможения для линейно изменяющегося ускорения (рис. 2.28) работают аналогично. Вместо (2.35), (2.36) в данном случае будут квадратичная и кубичная зависимости от времени. В алгоритмах также придется фиксировать точки перегиба парабол (рис. 2.28) изменения скоро- стей разгона и торможения.

24. Задача стабилизации рабочего органа исполнительного механизма относительно расчётной траектории: постановка задачи, основные определения, диагностические сообщения.

Задача стабилизации ИМ – это задача управления с обратной связью [17]. Далее будем рассматривать многомерную следящую систему, используемую в процессе формообразования. Следящую систему целесообразно формировать на основе принципа подчиненного управления.

Запишем математическую модель ИМ (2.43) в операторной форме:

(2.47)

где р – оператор дифференцирования ., -возмущающие силы, – вектор управляющих сил. A – симметричная матрица инерции ИМ

Так как матрица инерции A не зависит от скорости , на основе уравнений (2.47) можно построить 2 линейных подчиненных контура управления скоростью и положением 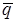соответственно.

В качестве критерия оптимальности следует задаться переходным процессом требуемого качества (например, предельно допустимым перерегулированием и временем переходного процесса при скачкообразных входном и возмущающем воздействиях).