Решение.

,

или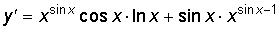

5.1. Понятие производной высшего порядка

Пусть функция 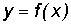определена и дифференцируема на некотором промежутке X, тогда ее производная также является функцией от x на этом промежутке. Если имеет производную на промежутке X, то эта производная называется производной второго порядкафункции y = f(x) и обозначается: y'' или .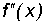

Итак,

Производная от производной второго порядка называетсяпроизводной третьего порядкаи обозначается: y''' или .

Вообще, производной n-го порядка называется производная от производной -го порядка и обозначается: y⁽ⁿ⁾ или f ⁽ⁿ⁾(x). Итак,

f ⁽ⁿ⁾(x) = (f ^(n-1)(x))'.

Производные y'', y''', ... называются производными высших порядков.

Пример 5.1. . Найти и .

Решение.

= = ,

= – ,

= = ,

= = = .

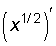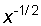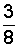
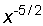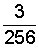Пример 5.2. Найти производную n-го порядка для функции .