Решение. 4.3. Дифференцирование функций, заданных параме

.

.

Отсюда .

4.3. Дифференцирование функций, заданных параметрически

Рассмотрим задание линии на плоскости, при котором переменные x, y являются функциями третьей переменной t (называемой параметром):

(4.3)

Каждому значению t из некоторого интервала соответствуют определенные значения x и y, а, следовательно, определенная точка M плоскости. Когда t пробегает все значения из заданного интервала, то точка M описывает некоторую линию L. Уравнения (4.3) называютсяпараметрическими уравнениями линии L.

Если функция на некотором интервале изменения t имеет обратную функцию 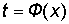, то подставляя это выражение в уравнение , получим , которое задает y как функцию от x.

Пусть , имеют производные, причем . По правилу дифференцирования сложной функции . На основании правила дифференцирования обратной функции , имеем:

(4.4)

Полученная формула (4.4) позволяет находить производные для функций, заданных параметрически.

Пример 4.3. Пусть функция y, зависящая от x, задана параметрически:

.

Найти .