СПРОС НА ТРУД ФИРМ С РАЗЛИЧНОЙ ЦЕЛЕВОЙ ФУНКЦИЕЙ.

Существует множество альтернативных целевых функций фирм. Рассм-м 2 из них:

1. максимизация полезности менеджера

2. максимизация доходов работников при самоуправлении.

1.Модель максимизации полезности менеджера состоит в том, что он может преследовать свои цели, отличные от максимизации прибыли фирмы. В модели предполагается, что полезность менеджера зависит от его компетенции, т.е. от отчетных прибылей фирмы (I) и расходов на персонал ему подчиненный (π*), а также от власти менеджера (S). Так как прибыль входит в функцию полезности менеджера, то он должен будет обеспечивать свою максимизацию в пространстве 'власть-прибыль'. Для каждого уровня расходов на персонал всегда существует какая-то кривая максимального отчетного периода, которая может быть достигнута фирмой. Предположим, что эта кривая Sπ*. Кривые безразличия менеджеров могут быть представлены некоторыми линиями (они соответствую разному уровню прибыли), которые показывают выбор между отчетными прибылями и количеством персонала, находящегося в подчинении у менеджера.

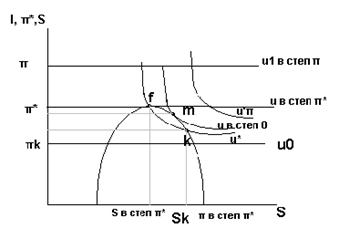Тогда этим величинам должны соответствовать некоторые кривые безразличия, одна из которых проходит через т. (S^π*; u^π*) принадлежащую u*. Равновесное положение соответствует условию нахождения в максимальной точке прибыли. Каждая кривая безразличия, лежащая ниже кривой u* , будет пересекать функцию прибыли в точке, имеющей худшие сочетания по уровню прибыли и уровню власти менеджера.

Но, если мы перемещаемся по уровню полезности вверх, переходя с u* на кривую u⁰ , то происходит падение уровня прибыли фирмы при одновременной максимизации уровня власти менеджера. Здесь возможны 2 варианта: а) менеджер- владелец фирмы.→ тогда он будет извлекать полезность не из увеличения количества привлеченного персонала, а из увеличения уровня прибыли. Именно в этом случае кривые безразличия занимают горизонтальное положение, потому что ему важно только какой уровень прибыли он получает и его не интересует на какое количество работников распространяется его власть. Точка, соответствующая уровню власти S^π* дает ему максимум прибыли.

б) фирмой руководит профессиональный менеджер, не являющийся владельцем. Для того, чтобы заставить его максимизировать прибыль, находясь в точке f,когда он окажется при уровне власти S^π* ,можно только ограничив жестко его возможности по количеству привлекаемого персонала, в каждом другом случае он или уйдет в точку К, увеличив свой уровень власти до S_k , или, если владелец определит допустимый уровень прибыли πm < чем его оптимальная величина π*, то наемный менеджер будет максимизировать свою полезность перейдя на более высокую кривую безразличия (u⁰), пересекающую линию прибыли в точке m, при этом его уровень власти S_м будет > чем в оптимуме, но < чем в точке К (S^π*< S_м< S_k). Если владелец заинтересован в сохранении этого менеджера на своей фирме, то он для себя должен определять необходимое ему сочетание уровня отчетных прибылей фирмы и власти менеджера.

2. Модель фирмы, управляемой работниками (с самоуправлением) характеризуется тем, что работники одновременно являются и собственниками и в этой модели предполагается, что в краткосрочном периоде целевой функцией фирмы является максимизация среднего дохода на одного работника фирмы. Предположим, что используемая рабочая сила однородна, а доля оплаты одного работника (W) состоит из 2х частей: из з/п (w) и из той части прибыли, которая приходится на одного работника (π/L), тогда доход W = w + π/L и целевая функция (y=f(L)) в этом случае безусловно будет зависеть от количества нанимаемых работников, потому что мы говорим о краткосрочном периоде. Тогда определим уровень производства и занятости на фирме, при которых доход работника будет максимизироваться. Так как эта величина зависит от соотношения π/L, то, если мы обозначим за i уровень общей выплаты своим работникам из прибыли фирмы, то π/L = P ×Y/L – w – i/L → π = PY – wL – i (где P – общая выработка; w – з/п; i – выплаты из прибыли, Y/L – производительность труда; i/L- доля выплат из прибыли одного работника).

Рассмотрим производство, связанное с количеством используемого труда и дохода работников, занятых на фирме. В этом случае мы можем построить кривые, одна из которых соответствует уровню дохода одного работника. С =w + i/L , который является убывающим при повышении количества занятых работников на фирме. А вторую кривую возьмем, соответствующую стоимости продукции, производимой одним работником, т.е.

P ×Y/L = R. Эта функция также убывающая, но в отличие от функции дохода она будет выпуклой. И равновесие в уровне прибыли будет достигаться на максимальном расстоянии между данными кривыми, т.е. между кривой дохода на одного работника и кривой средних издержек на него.

Рассмотрим, что происходит с равновесием, если меняется или уровень % от прибыли, выплачиваемого работнику в коллективе (а), или цена за единицу изделий(б):

(а) изменяется % (I) – изменение этой ставки влияет на издержки фирмы. Тогда объем выпуска и занятости будет меняться в одном направлении с изменением этой величины (↑ I → ↑ занятость L → ↑ Y и наоборот). На графике такое положение будет соответствовать сдвигу из т L* в какую-то т L1, при которой расстояние между кривыми сокращается и происходит снижение общей разности, остающейся в распоряжении фирмы, причем возрастание числа занятых при этом будет сопровождаться более быстрым изменением производительности труда Y/L, чем скорость увеличения объема выпуска продукции за счет наращивания числа занятых на фирме.

(б) изменится цена за единицу изделий. Значит, объем выпуска и величина затраченного труда будут меняться в направлении противоположном с изменением цены на продукцию.(P↑, L↓, Y ↓). Но при этом при ↑Р должен ↑ и угол наклона кривой R, которая напрямую зависит от цены на продукцию. =>, мы должны из точки оптимума перейти в точку, где угол наклона касательной больше, и в разности быстрее растет значение производной, чем производительность труда и потому кривая предложения продукта, всвязи с неустойчивостью рыночного равновесия, может приобретать обратный изгиб.