Государственный экзамен. 1. Многомерные задачи оптимизации.

1. Многомерные задачи оптимизации.

2. Основные задачи теории систем.

3. Реляционная модель данных основные понятия.

4. Объектно-ориентированный подход

5. Имитационное моделирование и компьютерное моделирование. Основные особенности имитационных моделей.

6. Пассивный режим FTP.

1)Многомерные задачи оптимизации.

Типичная многомерная задача оптимизации – задача выбора оптимальных (наилучших) условий химического производства. Здесь целевая функция – выход интересующего нас химического продукта – зависит от состава сырья, от температуры, давления, имеющихся катализаторов и ряда других факторов

Дана целевая функция f (x) =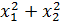 , которая графически представляет собой поверхность параболоида вращения(рис1).

Проведем сечения поверхности равно отстоящими плоскостями, которые параллельны плоскости изменения переменных x1 и x2. Линии этих сечений проецируем на плоскость изменения переменных. Получим концентрические окружности(рис.2). Эти линии называются линиями уровня или линиями постоянных значений. Основная характеристика любой из линий это то, что в любой точке этой линии значение функции постоянно.

Рис.1Методы многомерной оптимизации. Параболоид вращения

Рассечем заданную поверхность функции тремя плоскостями по уровням.

Тогда линии уровня будут представлены уравнениями:

;

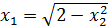или окружностями с соответствующими радиусами:

;

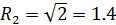Рис.2Методы многомерной оптимизации. Концентрические окружности

Все методы многомерной оптимизации делятся на два класса:

1) Градиентные

2) Безградиентные