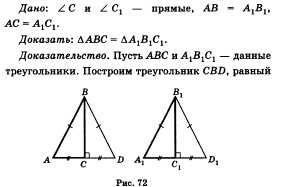
Признак равенства прямоугольных треугольников.

Так как в прямоугольном треугольнике угол между двумя катетами — прямой, а любые два прямых угла равны, то из первого признака равенства треугольников следует, что:

если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

Из второго признака равенства треугольников следует, что:

если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

Рассмотрим еще два признака равенства прямоугольных треугольников:

если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Доказательство. Из теоремы о сумме углов треугольника следует, что в этих треугольниках два других острых угла также равны, поэтому они равны по второму признаку равенства треугольников, т. е. по стороне (гипотенузе) и двум прилежащим к ней углам.

[П] Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

81. Задача по теме «Векторы».

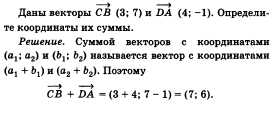
82. Задача по теме «Окружность, вписанная в треугольник».

Определите вид треугольника, если центр вписанной в него окружности совпадает с центром описанной около него окружности.

Решение. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник, а точка пересечения его серединных перпендикуляров — центром окружности, описанной около этого треугольника.

Из теоремы о медиане равнобедренного треугольника следует, что только в равностороннем треугольнике биссектрисы углов треугольника совпадают с серединными перпендикулярами. Значит, центр окружности, вписанной в треугольник, совпадает с центром описанной около него окружности только для равностороннего треугольника.