Построение с помощью циркуля и линейки перпендикулярной прямой.

Дано: .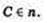

Построить прямую, перпендикулярную прямой п и проходящую через данную точку С.

Построение (рис. 48).

Проведем окружность произвольного радиуса с центром в точке С. Пусть В is. A — точки пересечения этой окружности с прямой л (постр. 2). Из точек В и А радиусом АВ проведем окружность, точку пересечения этих двух окружностей обозначим через О (постр. 3), проведем прямую СО (постр. 4). Перпендикулярность прямых СО и п следует из равенства треугольников АОС и ВОС.



Дано: .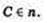

Построить прямую, перпендикулярную прямой п и проходящую через данную точку С.

Построение (рис. 49).

Проведем окружность произвольного радиуса с центром в точке С. Пусть В . A — точки пересечения этой окружности с прямой п (постр. 2). Из точек Б и А тем же радиусом проведем окружности и точки пересечения этих двух окружностей обозначим через С1 и С (постр. 3). Проведем прямую C1C (постр. 4).

Докажем перпендикулярность прямых СгС и п. Точку пересечения прямых CjC и п обозначим через О. Треугольники АСЕ иАСВ равны по третьему признаку равенства треугольников. Поэтому СОВ = = CAO. Тогда треугольники САО и С1АО равны по первому признаку равенства треугольников. Отсюда следует, что углы СОА и СОА равны. А так как они смежные, то они прямые. Следовательно, СО — перпендикуляр, опущенный из точки С на прямую п.