Метод контурных токов

При расчете сложных цепей методом узловых и контурных уравнений (по законам Кирхгофа) необходимо решать систему из большого количества уравнений, что значительно затрудняет вы­числения.

Так, для схемы рис. 4.13 необходимо составить и рассчитать систему из 7-ми уравнений.

Ту же задачу можно решить, записав только 4 уравнения по второму закону Кирхгофа, если воспользоваться методом контур­ных токов.

Суть метода состоит в том, что в схеме выделяют т независимых контуров, в каждом из которых произвольно направлены (см. пунктирные стрелки) контурные токи I₁ I_II, I_ш, I_IV.

Контурный ток — это расчетная величина, измерить которую невозможно.

Как видно из рис. 4.13, отдельные ветви схемы входят в два i смежных контура. Действительный ток в такой ветви определяет­ся алгебраической суммой контурных токов смежных контуров.

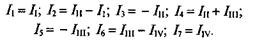Таким образом

Для определения контурных токов составляют т уравнений по второму закону Кирхгофа. В каждое уравнение входит алгебраическая сумма ЭДС, включенных в данный контур (по одну сторо­ну от знака равенства), и общее падение напряжения в данном контуре, созданное контурным током данного контура и контур­ными токами смежных контуров (по другую сторону знака равен­ства).

Решением системы уравнений вычисляются значения контурных токов, которые и определяют действительные токи в каждой и схемы (рис. 4.13).