Цепь с емкостью

Вели конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора проходит в цепи очень короткое время, пока напряжение на конденсаторе U_с не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I= 0).

Вели же конденсатор подключить к источнику с синусоидальном напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжение на конденсаторе U_c отстает по фазе от напряжения источника Ври зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение и= U_msinώt, то в цепи конденсатора проходит ток I (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90° = π/2l

Следовательно, напряжение отстает по фазе от тока на 90° = π/2 (рис.11.66)

Если уравнение (11.17) разделить на √2 =1,41,то получится равенство I= UώC или

Эторавенство (11.19а) и является математическим выражением законаОма для цепи переменного тока с емкостью. Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:

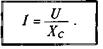
Тогдазакон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11.5а).

37. Неразветвленная RL-цепь.

38. Неразветвленная RC-цепь.

39. Неразветвленная RLC-цепь.

40. Построение векторно-топографической диаграммы и нахождение по ней напряжений от­дельных участков.

41. Резонанс напряжений.

42. Расчет цепи, состоящей из параллельно включенных активного индуктивного и емкостно­го сопротивлений.