Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью

Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток i=I_msinώt, то он создает падение напряже­ния на всех участках цепи: u_а= U_masinώt, u_L= U_mLsin (ώt +π/2) и

u_с= U_msin(ώt-π/2).

Мгновенное значение напряжения цепи определяется по фор­муле

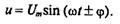Так как в рассматриваемой цепи включены два реактивных со­противления X_L и Х_с, то возможны три режима работы цепи: l)X_L>X_c;2)X_L<X_c;3)X_L = Xc.

Векторная диаграмма цепи для режима X_L>Х_с изображена на рис. 12.46

Знак перед углом сдвига фаз φ зависит от режима работы цепи. Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), 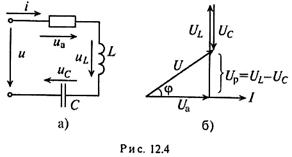т.е. U_L> U_c, то цепь имеет индуктивный характер и напряжение U опережает по фазе ток I(+φ).

Если в цепи преобладает емкостное напряжение (сопротивление), т.е. U_L< U_c, то цепь имеет емкостной характер и напряже­ние U отстает по фазе от тока I(—φ) 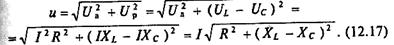Из векторной диаграммы (рис. 12.46) следует

Сопротивление R может включать в себя сопротивление само­стоятельного резистора или активное сопротивление реальной катушки и конденсатора.

Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:

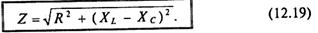
_Где Z — полное (или кажущееся) сопротивление неразветвлен­ной цепи с R, L и С, т. е.

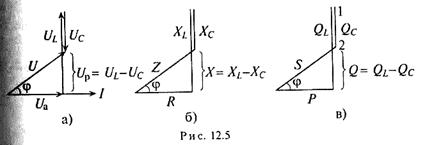
На рис. 12.5 изображены треугольники напряжений, сопротив­лений и мощностей для рассматриваемой цепи.

Знак и значение угла φ можно определить из треугольника со­противлений (рис. 12.56):

Из выражений (12.20) и (12.21) видно, что если X_L>Х_с, то угол φ положителен (+φ), если X_L<X_C, то угол ф отрицательный (-φ).

Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности P=Scosφ имеется реактивная мощность Q=S sinφ. Кроме того, в цепи происходит колебание мощности (меньшей из двух реактивных, в нашем случае U_c ) между электрическим полем конденсатора С и магнитным полем катушки индуктивности L, так как мощности Q_L и Q_c изменяются в противофазе. Но эта мощность (1—2 на рис. 12.5в) не считается реактивной, так как она не загружает источник и провода.

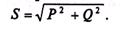Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= Q_L - Q_c. Эта реактивная мощность (энергия) колеблется между источ­ником и магнитным полем катушки индуктивности, так как Q_l>Q_c

Полная мощность цепи определяется по формуле

43. Расчет разветвленной цепи методом проводимостей.

44. Резонанс токов.

45. Значение коэффициента мощности в электроэнергетике.

46. Комплексные числа, действия над комплексными числами.

47. Комплексное представление электрических величин: тока, напряжения_, сопротивления, мощности, проводимости.

48. Расчет последовательной RLC - цепи комплексным методом.

49. Расчет параллельной RLC — цепи комплексным методом.