
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ТЕСТ З ТЕМИ «Інтегральне числення
⇐ ПредыдущаяСтр 11 из 11
функцій однієї змінної»
| Невизначений інтеграл. Теоретичні запитання | |
| 1. | Якій умові повинна задовольняти первісна  від функції від функції  на відрізку на відрізку  ? ?
|
| а) | 
|
| б) | 
|
| в) | 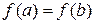
|
| г) | 
|
| д) | 
|
| 2. | Чому дорівнює різниця між двома первісними  і і  від однієї функції від однієї функції  на відрізку на відрізку  ? ?
|
| а) | 
|
| б) | функції 
|
| в) | 
|
| г) | 
|
| д) | сталому числу |
| 3. | Що називається невизначеним інтегралом від функції  , якщо , якщо  – первісна для – первісна для  , а , а  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 4. | Чому дорівнює похідна від невизначеного інтегралу,якщо  є первісною для є первісною для  , а , а  ? ?
|
| а) | підінтегральному виразу 
|
| б) | 
|
| в) | підінтегральній функції 
|
| г) | 
|
| д) | 
|
| 5. | Чому дорівнює диференціал від невизначеного інтеграла  , якщо , якщо  є первісною для є первісною для  , а , а  ? ?
|
| а) | 
|
| б) | підінтегральному виразу 
|
| в) | підінтегральній функції 
|
| г) | 
|
| д) | 
|
| 6. | Чому дорівнює невизначений інтеграл від диференціала деякої функції  , якщо , якщо  є первісною для є первісною для  , а , а  ? ?
|
| а) | 
|
| б) | 
|
| в) | підінтегральній функції 
|
| г) | |
| д) | 
|
| 7. | Вкажіть вірне формулювання теореми про інваріантність формул інтегрування. |
| а) |  , де , де  , , 
|
| б) |  , якщо , якщо  і і  – довільна функція, що має неперервну похідну – довільна функція, що має неперервну похідну
|
| в) |  = = 
|
| г) |  = =  , де , де  є первісною неперервної функції є первісною неперервної функції 
|
| д) |  , де , де  є первісною неперервної функції є первісною неперервної функції  , , 
|
| 8. | Чому дорівнює інтеграл  , якщо , якщо  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 9. | Чому дорівнює інтеграл  , якщо , якщо  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 10. | В яких формулах таблиці інтегралів не допущена помилка? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 11. | В яких формулах таблиці інтегралів допущена помилка? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 12. | Яка з функцій має похідну  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 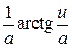
|
| 13. | Яка з функцій має похідну  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 14. | Яка формула називається формулою інтегрування частинами невизначеного інтеграла? |
| а) |  , де , де  , , 
|
| б) |  , якщо , якщо  і і  – довільна функція, що має неперервну похідну. – довільна функція, що має неперервну похідну.
|
| в) |  = = 
|
| г) |  = =  , де , де  є первісною неперервної функції є первісною неперервної функції 
|
| д) |  , де , де  є первісною неперервної функції є первісною неперервної функції  , , 
|
| 15. | Вкажіть, в яких з наведених інтегралів при обчисленні треба застосовувати формулу інтегрування частинами? |
| а) |  , де , де  – многочлен степені – многочлен степені 
|
| б) | 
|
| в) | 
|
| г) |  , де , де  – многочлен степені – многочлен степені 
|
| д) |  , де , де  – многочлен степені – многочлен степені 
|
| 16. | Для зображення підінтегрального раціонального дробу у вигляді найпростіших дробів необхідно: а) знайти корені знаменника; б) встановити, чи є правильним цей дріб ; в) розкласти знаменник на множники. Вкажіть правильну послідовність дій. |
| а) | в), б), а) |
| б) | б), в), а) |
| в) | б), а), в) |
| г) | а), б), в) |
| д) | в), а), б) |
| 17. | Вкажіть вигляд найпростішого раціонального дробу, при інтегруванні якого одержується результат  . .
|
| а) | 
|
| б) |  , , 
|
| в) | 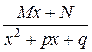 за умови за умови 
|
| г) |  за умови за умови  , , 
|
| д) | 
|
| 18. | Який тип має найпростіший підінтегральний дріб, якщо у нього  є коренем знаменника кратності є коренем знаменника кратності  , ,  ? ?
|
| а) | I тип: 
|
| б) | II тип:  , , 
|
| в) | III тип: 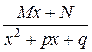 , , 
|
| г) | IV тип:  , ,  , , 
|
| д) | I і II типи: 
|
| 19. | Для обчислення інтеграла  треба зробити підстановку треба зробити підстановку  . Чому потрібно дорівнювати . Чому потрібно дорівнювати  ? ?
|
| а) | Найменшому загальному кратному знаменників дробів  . .
|
| б) | Найменшому загальному кратному чисельників дробів  . .
|
| в) | Найбільшому загальному дільнику знаменників дробів  . .
|
| г) | Найбільшому з чисел  . .
|
| д) | Найменшому з чисел  . .
|
| 20. | Якими формулами визначається універсальна тригонометрична підстановка? |
| а) |  , ,  , , 
|
| б) |  , , 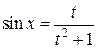 , , 
|
| в) |  , ,  , , 
|
| г) |  , ,  , , 
|
| д) |  , ,  , , 
|
| 21. | Коли використовуються формули зниження степеня при обчисленні інтеграла  ? ?
|
| а) | якщо  , , 
|
| б) | якщо  , , 
|
| в) | якщо  , , 
|
| г) | якщо  , , 
|
| д) | якщо  , , 
|
| 22. | Коли використовується заміна змінної  при обчисленні інтеграла при обчисленні інтеграла  ? ?
|
| а) | якщо  – довільне число, – довільне число, 
|
| б) | якщо  , ,  – довільне число – довільне число
|
| в) | якщо  , , 
|
| г) | якщо  , ,  – довільне число – довільне число
|
| д) | якщо  – довільне число, – довільне число, 
|
| 23. | Який вигляд має підінтегральна функція у випадку використання тригонометричної підстановки  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 24. | Який вигляд має підінтегральна функція у випадку використання тригонометричної підстановки  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 25. | Який вигляд має підінтегральна функція у випадку використання тригонометричної підстановки  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| Невизначений інтеграл. Практичні завдання | |
| 26. | Чому дорівнює похідна від інтеграла  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 27. | Графік якої первісної функції  проходить через точку з координатами проходить через точку з координатами  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 28. | Чому дорівнює інтеграл  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 29. | Вкажіть правильну відповідь при обчисленні інтеграла  . .
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 30. | Вкажіть правильну відповідь при обчисленні інтеграла  . .
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 31. | Які табличні інтеграли використовуються при обчисленні інтеграла  ? ?
|
| а) | 
|
| б) |  
|
| в) | 
|
| г) | 
|
| д) | 
|
| 32. | Які табличні інтеграли використовуються при обчисленні інтеграла  ? ?
|
| а) | 
|
| б) |  
|
| в) | 
|
| г) | 
|
| д) | 
|
| 33. | Які табличні інтеграли використовуються при обчисленні інтеграла  ? ?
|
| а) | 
|
| б) |  
|
| в) | 
|
| г) | 
|
| д) | 
|
| 34. | Які табличні інтеграли використовуються при обчисленні інтеграла  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 35. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) |  
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 36. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) |  
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 37. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) |  
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 38. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) |  
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 39. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) |  
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 40. | Вкажіть, за допомогою яких табличних інтегралів знаходять інтеграл  . Для цього використовуйте метод підведення під знак диференціала. . Для цього використовуйте метод підведення під знак диференціала.
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 41. | В яких з наведених інтегралів доцільно зробити універсальну тригонометричну підстановку  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 42. | Яким методом треба обчислити інтеграл  ? ?
|
| а) | За допомогою заміни змінної. |
| б) | За допомогою універсальної тригонометричної підстановки. |
| в) | За допомогою формули інтегрування частинами. |
| г) | За допомогою метода безпосереднього інтегрування. |
| д) | За допомогою метода підведення під знак диференціала. |
| 43. | Що при обчисленні інтеграла  за допомогою формули інтегрування частинами вибирають за за допомогою формули інтегрування частинами вибирають за  , а що за , а що за  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 44. | Що при обчисленні інтеграла  за допомогою формули інтегрування частинами вибирають за за допомогою формули інтегрування частинами вибирають за  , а що за , а що за  ? ?
|
| а) |  , , 
|
| б) |  , , 
|
| в) |  , , 
|
| г) |  , , 
|
| д) |  , , 
|
| 45. | Вкажіть правильну відповідь при обчисленні інтеграла  . .
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 46. | Вкажіть правильну відповідь при обчисленні інтеграла  . .
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 47. | Яким чином в інтегралі  необхідно розкласти підінтегральний дріб на найпростіші дроби? необхідно розкласти підінтегральний дріб на найпростіші дроби?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 48. | Визначити, як подається інтеграл  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 49. | Яка підстановка раціоналізує інтеграл  ? ?
|
| а) | 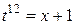
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 50. | Яка підстановка раціоналізує інтеграл  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| Визначений інтеграл. Теоретичні запитання | |
| 51. | Якими лініями обмежена фігура, яку називають криволінійною трапецією? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 52. | В якому з наведених властивостей визначеного інтеграла допущена помилка? |
| а) | 
|
| б) | Якщо  , то , то  . .
|
| в) | 
|
| г) | 
|
| д) | 
|
| 53. | Яке з наведених властивостей визначеного інтеграла називають теоремою про середнє значення функції? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 
|
| 54. | Якщо  , то яке значення має , то яке значення має  ? ?
|
| а) | Довільне. |
| б) | Найменше значення функції  на на  . .
|
| в) | Найбільше значення функції  на на  . .
|
| г) | Середнє значення функції  на на  . .
|
| д) | Додатне значення функції  на на  . .
|
| 55. | За яких умов справедлива формула заміни змінної в визначеному інтегралі  ? ?
|
| а) |  і і  – неперервні на – неперервні на  визначена і неперервна на визначена і неперервна на 
|
| б) |  і і  – неперервні на – неперервні на  , ,  визначена і неперервна на визначена і неперервна на 
|
| в) |  , ,  , ,  визначені і неперервні на визначені і неперервні на 
|
| г) |  , ,  визначені і неперервні на визначені і неперервні на 
|
| д) |  , ,  неперервна на неперервна на 
|
| 56. | Якими лініями обмежена фігуру, котру називають криволінійним сектором? |
| а) | 
|
| б) | 
|
| в) | 
|
| г) | 
|
| д) | 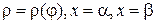
|
| 57. | Яким умовам повинні задовольняти функції  та та  , щоб була справедлива формула Н'ютона-Лейбница , щоб була справедлива формула Н'ютона-Лейбница  ? ?
|
| а) |  необмежена на необмежена на  , ,  – первісна для – первісна для 
|
| б) |  неперервна на неперервна на 
|
| в) |  визначена на визначена на  , ,  – первісна для – первісна для 
|
| г) |  неперервна на неперервна на  , ,  – первісна для – первісна для 
|
| д) |  і і  – довільні неперервні на – довільні неперервні на  функції функції
|
| 58. | Чому дорівнює  ? ?
|
| а) | 
|
| б) | |
| в) | 
|
| г) | 
|
| д) | 
|
| 59. | Чому дорівнює  ? ?
|
| а) | 
|
| б) | |
| в) | 
|
| г) | 
|
| д) | 
|
| 60. | Якій умові повинна задовольняти підінтегральна функція  , щоб виконувалась рівність , щоб виконувалась рівність  ? ?
|
| а) | 
|
| б) | 
|
| в) | 
|
| г) |  – парна функція – парна функція
|
| д) |  – непарна функція – непарна функція
|
| 61. | Якій умові повинна задовольняти підінтегральна функція  , щоб виконувалась рівність , щоб виконувалась рівність  ? ?
|
| а) |  – парна функція – парна функція
|
| б) |  – непарна функція – непарна функція
|
| в) |  – невід'ємна функція – невід'ємна функція
|
| г) | 
|
| д) | 
|
| 62. | Який вигляд має формула інтегрування частинами у визначеному інтегралі? |
| а) | 
|
| б) | |
Дата добавления: 2015-04-21; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |