Круговая номограмма Вольперта. Описание номограммы. Методика определения полного сопротивления комплексной нагрузки. Согласование линии передачи и сопротивлений

При пересчетах сопротивлений и проводимостей в отрезках линий передачи удобно использовать круговую номограмму, предложенную в 1939 г. советским ученым А. Р. Вольпертом.

Основы для построения круговой номограммы составляют формулы для расчета коэф-та отражения: и для трансформации сопротивлений:

Коэффициент отражения на круговой номограмме (рис. 1.20) изображается в полярной системе коорди­нат, причем радиусу соответствует модуль коэффициента отраже­ния, а полярному углу f — удвоенное электрическое расстояние вдоль линии передачи, т.е. фазовый угол коэффициента отражения . Для пассивных устройств модуль коэффициента отражения не превышает единицы, поэтому номограмма ограничена внешней окружностью единичного радиуса |р| = 1. Центр номограммы со­ответствует нулевому коэффи­циенту отражения. Электриче­ская длина отсчитывается на номограмме в виде углов пово­рота радиуса-вектора, враща­ющегося вокруг центра номо­граммы. Повороту по часовой стрелке соответствует переме­щение наблюдаемого сечения в линии передачи в сторону ге­нератора. Полный оборот соот­ветствует полуволновому рас­стоянию вдоль линии. Четверть­волновое расстояние определя­ется половиной оборота. Линии постоянных фаз коэффициента отражения, т.е. радиусы, на номограмме обычно не изобра­жают, а вместо линий постоян­ных модулей коэффициента от­ражения наносят штриховые концентрические окружности постоянных КБВ. Часто круго­вая номограмма дополняется поворотной радиальной шкалой, на которую наряду с делениями КБВ (или КСВ) наносят также деления модуля коэффициента от­ражения. Такая шкала изображена отдельно на рис. 1.20.

Кроме полярных координат для коэффициента отражения и КБВ при построении круговой номограммы используется вторая координатная сетка, образуемая пересечением системы линий по­стоянных нормированных активных сопротивлений г (или активных проводимостей g) и системы линий постоянных нормированных реактивных сопротивлений х (или проводимостей b). Линии по­стоянных г являются окружностями радиусами 1/(1 + r) с центра­ми, расположенными на горизонтальной оси симметрии. Все окруж­ности постоянных r соприкасаются между собой в точке В номограммы (рис. 1.20). Характерной является окружность r=1, проходящая через центр номограммы. Линии постоянных х являются также окружностями, их радиусы равны 1/х, а центры располага­ется на вертикальной прямой, проходящей через точку В. Линии отрицательных значений х лежат в нижней половине номограммы а линии положительных значений х — в верхней. На горизонтальной оси симметрии номограммы реактивные сопротивления равны нулю.

Для перехода от безразмерного нормированного сопротивления к реальному (Ом) необходимо: .

Методика определения полного сопротивленияна примере прямоугольного волновода.

1)

2) Измерить длину волны: 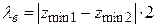. Зафиксировать координату .

3) Вместо короткозамыкателя ставится исследуемый отрезок волновода с согласованной нагрузкой. В качестве исследуемых неоднородностей могут выступать разомкнутые и замкнутые штыри, различные диафрагмы.

При исследовании отрезка местоположения неоднородностей и КЗ поршня должны совпадать. В противном случае вводится поправка (при смещении влево – со знаком “+”, а при смещении вправо – “-“).

4) Измеряется и высчитывается КСВ ( ) и определяется минимум, ближайший к минимуму, отмеченному в пункте 2.

5) Определяется .

6) Определяется .

7) По номограмме Вольперта через КСВ по линейке или (по шкале на окружности) определяется местоположение точки z₁. Через эту точку проходит окружность (действительная часть) и дуга (реактивная часть).

С учетом конструкции определяем знак перед мнимой частью: “+” или ”-”.

8) Домножаем полученное выражение на волновое сопротивление ЛП.

Матричное описание многополюсников СВЧ. Понятие многополюсников СВЧ. Матрица многополюсника. Классический и волновой подходы при электрическом описании многополюсника. Матрица проводимостей и сопротивлений. Матрица рассеяния. Связь между матрицами рассеяния, проводимостей и сопротивлений.

Под многополюс­ником СВЧ понимают любую комбинацию проводников, диэлект­риков и других элементов СВЧ, имеющую несколько входов в виде поперечных сечений линий передачи с заданными типами волн в каждой линии. Сечения входов многополюсника называют плоско­стями отсчета фаз.

Особое внимание уделяется микрополосковым пассивным многополюсникам.

Линейные – свойства заполняющих сред не изменяются при изменении мощности ( ).

Пассивные – отсутствует усиление мощности и генерация; обычно мощность потерь высокая или равна 0.

Матрицы многополюсника выявляют взаимосвязи между элект­рическими режимами его входов. Режимы в плоскостях отсчета фаз многополюсника могут быть описаны как в терминах нормирован­ных напряжений падающих и отраженных волн — это так называе­мый волновой подход, так и в терминах полных нормированных на­пряжений и токов — это так называемый классический подход.

При волновом подходе для каждого входа m произвольного 2N-полюсника условимся называть падающими нормированные волны напряжения u_nm (размерностью ÖВт), распространяющиеся в сторону к многополюснику, и соответственно отраженными (или рассеянными) нормированные волны напряжения u_оm (размер­ностью ÖВт), распространяющиеся в сторону от многополюсника (рис. 3.1, а).

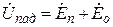; (при ).

При классическом подходе режимы каждого входа многополюс­ника задаются нормированными напряжениями u_m и нормирован­ными токами i_m, втекающими внутрь многополюсника (рис. 3.1, б).

; (при ).

; (при 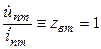). (1)

Поэтому в самом общем случае каждый вход многополюсника может быть описан любыми двумя параметрами, входящими в (1).