Связь между матрицами.

Любая матрица параметров многополюсника является его пол­ной внешней характеристикой. Выбор той или иной матрицы дик­туется удобством проведения расчетов элементов матриц или при­нятой методикой экспериментального определения параметров многополюсника. Все матрицы одного и того же многополюсника однозначно связаны между собой. Поэтому, зная одну из них, мож­но вычислить и остальные. Наиболее простая связь существует между матрицами сопротивлений и проводимо­стей — эти матрицы обратны одна по отношению к другой.

Чтобы установить взаимосвязь между матрицей рассеяния и матрицей сопротивлений (или проводимостей) и вообще между любыми двумя произвольными матрицами многополюсника, нужно использовать соотношения между напряжениями падающих и отраженных волн во входных линиях передачи, с одной стороны, и нормированными напряжениями и токами — с другой. Имея в ви­ду, что соотношения справедливы для всех входных линий многополюсника, их можно представить в объединенной матричной форме относительно столбцов напряжений и токов. Используем выражение (1):

При сложении уравнений: ; при вычитании уравнений: 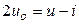. 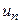, , 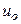, - матрицы-столбцы из N элементов (2).

Подставляя столбцы u_n и u_о из (2) в систему уравнений 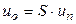, определяющую матрицу рассеяния, получаем: .

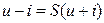Группируя в левой части равенства слагаемые с множителем u, можно записать 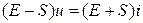, где Е - единичная матрица порядка N. Умножая это уравнение слева на матрицу 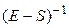, приходим к соотношению: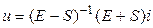

Сопоставления полученное выражение с системой уравнений для матрицы сопротивлений следует искомая формула связи матриц Z и S:

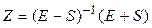. (3)

Из соотношения (3) следует, что матрица сопротивлений су­ществует не всегда — она оказывается неопределенной при обра­щении в нуль определителя матрицы, подлежащей обращению, т.е. при det (Е—S)=0.

Для матрицы проводимостей Y тем же путем, что и для матри­цы Z, можно получить выражение, связывающее ее с матрицей рас­сеяния (необходимо поменять знаки в скобках на противоположные):

. (4)

Из этого соотношения следует, что если определитель det (E+S)=0, то матрица проводимостей Y для многополюсника отсут­ствует. Например, непосредственной, проверкой можно установить, что обращаются в нуль det(Е—S) и det(E+S) для шестиполюсника в виде параллельного разветвления трех линий передачи. Это указывает на одновременное отсутствие матриц Z и Y для такого шестиполюсника.

Нормированные матрицы многополюсника. Соотношение нормировки для матрицы рассеяния и проводимостей. Сдвиг плоскостей отсчета фаз на входах многополюсника. Идеальная и реальная матрицы многополюсника.

Для подводящих линий соотношения нормировки напряжений и токов имеют вид 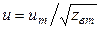, , 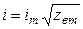где m - номер входа. Всей совокупности входных линий передачи 2N-полюсника соответствуют матричные соотношения нормировки: 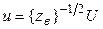; 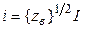,где 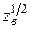- диагональная матрица, элементами диагонали кото­рой являются положительные числа , m=1,2,...,N. Матри­ца 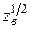- также диагональная матрица, элементы диагонали ко­торой равны .

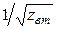Подставив столбцы u и i, определенные соотношениями норми­ровки, в систему уравнений и решив эту систему относительно столбца U, получим 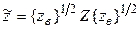, или .

Отсюда следует, что ненормированные столбцы напряжений и токов связаны между собой квадратной матрицей Z={Z_B}^1/2Z×{Z_B}^1/2, которая может быть названа ненормированной матрицей сопротивлений. Элементы этой матрицы имеют размерность Ом и связаны с соответствующими безразмерными элементами i_mn нор­мированной матрицы Z соотношением z_mn=z_mn(Z_BmZ_Bn)^1/2.

Аналогично вводится ненормированная матрица проводимостей:

, .

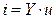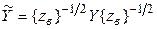Элементы матрицы Y (размерность См) связаны с безразмерными элементами нормированной матрицы проводимостей соотношением: .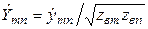

Ненормированные матрицы Z и Y применяются в теории много­элементных вибраторных и щелевых антенн.