Недиссипативные многополюсники.

Недиссипативными называют такие многополюсники, в которых отсутствуют внутренние потери электромагнитной энергии. Строго говоря, не существует абсолютно недиссипативных устройств СВЧ, любое устройство в той или иной степени расходует (напри­мер, преобразует в теплоту) часть проходящей через него мощно­сти СВЧ. Однако внутренние потери в большинстве случаев стре­мятся свести к минимуму и предельным случаем устройств с малы­ми потерями как раз и являются недиссипативные устройства. Малость потерь следует понимать таким образом, что они исчезающе малы на фоне общей мощности, подаваемой на входы 2N-полюсника. Пренебрежение внутренними потерями ведет к упроще­нию расчетных соотношений и поэтому оказывается полезным при анализе устройств.

Сформулируем свойство недиссипативности многопо­люсника в терминах матрицы сопротивлений. Мощность, поступа­ющая по каждой входной линии передачи:

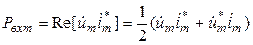. (1)

Суммируя мощности по всем входам 2N-полюсника и переходя к матричным обозначениям, получаем:

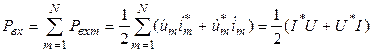. (2)

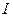Здесь и - матрицы-строки; и - матрицы-столбцы. Используя в (1) определение мат­рицы сопротивлений, учитывая правило транспонирования произведения матриц (АВ)_t = В_tА_t и требуя, чтобы P_ВХ=0, что должно иметь место в недиссипативном многополюснике, приходим к соотношению:

.

Равенство нулю входной мощности не должно зависеть от кон­кретного вида воздействия i на недиссипативный многополюсник. Это может быть только в том случае, если матрица сопротивлений удовлетворяет условию Z+Z_t*=0 или Z=–Zt*, где 0 – нулевая матрица порядка N.

Аналогичное условие недиссипативности многополюсника име­ет место и для матрицы проводимостей: Y+Yt* = 0 или Y=–Yt*.