Гидростат.давл и его свойства.

В покоящейся жидкости возможен лишь один вид напряжений – напряжения сжатия, т. е. гидростатическое давление.

1 св-во: На внешней поверхности гидростатическое давление всегда направлено по нормали, внутрь рассматриваемого объема жидкости.

2 св-во: В любой точке внутри жидкости давление по всем направлениям одинаково.

Для доказательства этого положения выде­лим в районе произвольно выбранной точки на­ходящейся внутри жидкости малый отсек жид­кости. Три взаимно перпенди­кулярные грани отсека будут параллельны ко­ординатным плоскостям, четвёртая грань распо­ложена под произвольным углом .

От­бросим массу жидкости, находящуюся с внеш­ней стороны поверхности тетраэдра, а действие отброшенной массы жидкости на выделенный отсек заменим силами, которые обеспечат равновесие в покоящейся жидкости. При такой замене мы сделали некоторое допущение, ввели сосредоточенные силы, действующие на грани отсека. Однако это допущ можно считать справедливым ввиду малости отсека. Тогда для обеспечения равновесия на от­сек жидкости должны действовать силы давления нормальные к граням отсека ; корме того, на этот же отсек жидкости будут действовать массовые силы характер действия которых определяется переносным движением, т.е. движе­нием сосуда, относительно которого покоится жидкость. Величина массовых сил будет пропорциональна массе жидкости в отсеке:

Запишем уравнение равновесия отсека жидкости в проекциях на оси координат.

Выразив силы через напряжения, уравнения равновесия будут иметь следующий вид:

где: - площадь наклонной грани отсека, 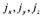- проекции ускорения переносного движения на оси координат.

учитывая, что:

Уравнения равновесия примут вид:

Пренебрегая малыми величинами, получим: