Давление жидкости на цилиндрическую поверхность.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС, простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсекеАОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскостьyOz.

Cила гидростатического давления на площадь S_x равна F_x = γ S_xh_c.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

F_x - R_x = 0 откуда F_x = R_x = γS_xh_c

Теперь спроецируем все силы на ось Оz:

R_x - G = 0 откуда R_x = G = γV

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давленияR=F, то делаем вывод, что

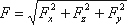
13. Ур-е Бернулли для

Рассмотрим элементарную струйку идеальной жидкости при установившемся движении, в которой выделим два сечения 1-1 и 2-2.Площади живых сечений потока обозначим dЙ1 и dЙ2. Положение центров тяжести этих сечений относительно произвольно расположенной линии сравнения (нулевой линии) 0- 0характеризуется величинами z1и z2. Давления и скорости жидкости в этих сечениях имеют значения P1, P2и u1, u2 соответственно.

Будем считать, что движение струйки жидкости происходит только под действием силы давления (внутреннее трение в жидкости отсутствует), а давление обладает свойствами статического и действует по нормали внутрь рассматриваемого объёма.

За малый промежуток времени dt частицы жидкости из 1-1 переместятся в 1'-1' на расстояние, равноеu1dt, а частицы из 2-2 в 2' - 2' на расстояние u2dt.

Согласно теореме кинетической энергии приращение энергии тела (в данном случае выделенного объёма жидкости) равно сумме работ всех действующих на него сил.

Работу в данном случае производят силы давления, действующие в рассматриваемых живых сечениях струйки 1-1 и 2-2, а также силы тяжести. Тогда работа сил давления в сечении 1-1 будет положительна, т.к. направление силы совпадает с направлением скорости струйки. Она будет равна произведению силы p1dЙ1 на путь u1dt:

Работа сил давления в сечении 2-2 будет отрицательной, т.к. направление силы противоположно направлению скорости. Её значение

Полная работа, выполненная силами давления, примет вид: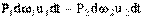

Работа сил тяжести равна изменению потенциальной энергии положения выделенного объёма жидкости при перемещении из сечения 1-1 в сечение 2-2. С учётом условия неразрывности потока и несжимаемости жидкости выделенные элементарные объёмы будут равны и, следовательно, будут равны их весаdG:

При перетекании от сечения 1-1 в сечение 2-2 центр тяжести выделенного объёма переместится на разность высот (z1 – z2) и работа, произведённая силами тяжести, составит: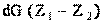

Проанализируем теперь изменение кинетической энергии рассматриваемого объёма элементарной струйки жидкости.

Приращение кинетической энергии выделенного объёма за dt равно разности его кинетических энергий в сечениях 1-1 и 2-2. Это приращение составит

Приравнивая приращение кинетической энергии сумме работ сил тяжести и сил давления, придём к виду:

Разделив обе части на вес dG, т.е. приведя уравнение к единичному весу, получим

После сокращения и преобразований придём к искомому виду

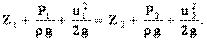
Если учесть, что сечения 1-1 и 2-2 выбраны произвольно, можно прийти к выводу, что сумма приведённых выше величин описывающих движение жидкости под действием сил давления и сил тяжести есть величина постоянная для элементарной струйки, т.е.

Таким образом, снова получено то же (ранее полученное интегрированием уравнений Эйлера) уравнение Бернулли для элементарной струйкиневязкой жидкости при установившемся движении под действием сил тяжести