Сила давления жидкости на плоскую стенку

Используем основное уравнение гидростатики для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом a (рис. 2.6). Вычислим силу давления Р, действующую со стороны жидкости на некоторый участок рассматриваемой стенки, ограниченный произвольным контуром и имеющий площадь, равную S.

Ось ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось оу - перпендикулярно этой линии в плоскости стенки.

Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS

(2.14)

где р₀ - давление на свободной поверхности; h - глубина расположения площадки dS. Для определении полной силы Р выполним интегрирование по всей площади S:

(2.15)

где y – ордината центра площадки dS.

Последний интеграл, как известно из механики, представляет собой статический момент площади S относительно оси ох и равен произведению этой площади на координату ее центра тяжести (точка С), т.е.

Следовательно,

здесь h_c – глубина расположения центра тяжести площади S), или

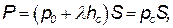
(2.16)

т.е. полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления в центре тяжести этой площади.

Если давление p₀ является атмосферным, то сила избыточного давления жидкости на плоскую стенку равна

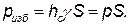
(2.17)

Найдем теперь положение центра давления, т.е. координату точки пересечения силы давления жидкости на стенку с плоскостью стенки.

Так как внешнее давление р₀ передается всем точкам площади S одинаково, то равнодействующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) применим уравнение механики, смысл которого заключается в том, что момент равнодействующей силы давления относительно оси оx равен сумме моментов составляющих сил, т.е.

где у_D – координата точки приложения силы Р_изб.

Рис. 2.6. Схема воздействия давления на твердую стенку

Выражая Р_изб и dР_изб через у_с и у, и определяя у_D, будем иметь

(2.18)

где

– момент инерции площади S относительно оси ox.

Учитывая, что

(2.19)

(J_x0 – момент инерции площади S относительно центральной оси, параллельной ох), окончательно получим

Таким образом, точка приложения силы Р_изб расположена ниже центра тяжести площади стенки; расстояние между ними равно

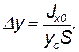
(2.20)

Если давление р₀ равно атмосферному и оно действует с обеих сторон стенки, то точка D и будет центром давления. Когда же р₀ является повышенным, то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: h_cgS и p₀S. При этом, чем больше вторая сила по сравнению с первой, тем, очевидно, ближе центр давления к центру тяжести площади S.

Выше было дано определение лишь одной координаты центра давления y_D. Для определения другой его координаты – x_D следует составить уравнение моментов относительно оси Оу.

В частном случае, когда стенка имеет прямоугольную форму. Причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится очень просто. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис. 2.6), центр тяжести которого находится на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на 1/3 b, считая снизу.

В авиационной технике приходится часто сталкиваться с действием силы давления жидкости на плоские стенки, например, на стенки поршней различных гидростатических машин и устройств, при этом давление р₀ обычно бывает настолько высоким, что центр давления можно считать совпадающим с центром тяжести площади стенки.