
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные уравнения гидравлики и газовой динамики
Основные понятия
Переходя к изучению вопросов движения жидкости, нужно заметить, что на первых порах мы будем рассматривать движение так называемой идеальной жидкости, т.е. такой воображаемой жидкости, которая совершенно лишена вязкости, и лишь потом перейдем к изучению реальных потоков. В такой невязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений – нормальное напряжение сжатия, т.е. гидромеханическое давление, или просто давление.
Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т.е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке внутри жидкости – по всем направлениям одинаково.
Течение жидкости может быть установившимся (стационарным) или неустановившимся (нестационарным).
| Установившееся течение – это течение неизменное по времени, при котором гидромеханическое давление и скорость являются функциями лишь координат, но не зависят от времени. |
Давление и скорость могут изменяться при перемещении частиц жидкости из одного положения в другое, но в данной неподвижной относительно русла точке величины давления и скорости при установившемся движении не меняются по времени.
Математически это можно записать так:
p=f1(x,y,z); u=f2(x,y,z)

| (3.1) |
где индексы у скорости означают проекции этой скорости на соответствующие оси, жестко связанные с руслом.
В общем случае неустановившегося течениядавление и скорость зависят как от координат, так и от времени, т.е.

| (3.2) |
Примерами неустановившегося течения жидкости могут служить постепенное опорожнение сосуда через отверстие в дне или движение жидкости во всасывающей или напорной трубе простого поршневого насоса, поршень которого совершает возвратно-поступательное движение.
Примеры установившегося течения: истечение жидкости из сосуда, в котором поддерживается постоянный уровень; движение жидкости в замкнутом трубопроводе, создаваемое работой центробежного насоса с постоянным числом оборотов.
Исследование установившихся течений гораздо проще, чем неустановившихся. В дальнейшем мы будем рассматривать главным образом установившиеся течения и лишь некоторые частные случаи неустановившегося течения.
Траектории частиц жидкости при установившемся течении являются неизменными по времени кривыми.
При неустановившемся течении траектории различных частиц, проходящих через данную точку пространства, будут иметь разную форму. Поэтому для рассмотрения картины течения, образующейся в каждый данный момент времени, вводится понятие линии тока.
| Линией тока называется такая линия в движущейся жидкости, касательные к которой в любой ее точке совпадают с направлением векторов скорости частиц, расположенных на этой линии в данный момент времени (рис. 3.1). |
Очевидно, что в условиях установившегося течения линия тока совпадает с траекторией и не изменяет своей формы с течением времени.
| Если в движущейся жидкости взять элементарный замкнутый контур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Часть потока, заключенная внутри трубки тока, называется струйкой (рис. 3.1). |
При стремлении поперечных размеров струйки к нулю струйка в пределе обращается в линию тока.
В любой точке боковой поверхности струйки, т.е. трубки тока, векторы скорости направлены по касательным, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, ни одна частица жидкости ни в одной точке трубки тока не может проникнуть внутрь струйки или выйти наружу. Трубка тока, таким образом, является как бы непроницаемой стенкой, а элементарная струйка представляет собой самостоятельный элементарный поток. Потоки конечных размеров мы будем на первых порах рассматривать как совокупность элементарных струек, т.е. течение будем предполагать струйным. Вследствие различия скоростей соседние струйки будут скользить одна по другой, не перемешиваясь друг с другом.

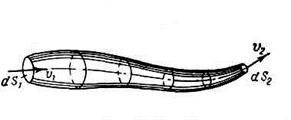
Рис. 3.1. Линия тока и элементарная струйка жидкости
| Живым сечением или просто сечением потока называется в общем случае поверхность в пределах потока, проведенная нормально к линиям тока. |
Обычно в потоках рассматривают такие участки, в которых струйки можно считать параллельными и, следовательно, живые сечения - плоскими.
Различают течения жидкости напорные и безнапорные.
| Напорными называют течения в закрытых руслах без свободной поверхности, а безнапорными- течения со свободной поверхностью. |
При напорных течениях давление вдоль потока обычно переменное при безнапорном - постоянное (чаще всего атмосферное). Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, течения в гидромашинах и других гидроагрегатах. Безнапорными являются течения в реках, открытых каналах и лотках. В данном курсе мы будем рассматривать почти исключительно течения напорные.
С вязкостью связано возникновение пограничного слоя при обтекании жидкостями твердых тел. Пусть поток жидкости с равномерным полем скорости uн=соnst набегает на поверхность тонкой плоской пластины и течет параллельно ей (рис. 3.2).
uн=30 м/с; Тн=293К; Рн=105 Па; Рабочее тело - воздух.

Рис. 3.2. Динамический пограничный слой
Молекулы жидкости, непосредственно прилегающие к поверхности твердого тела, прилипают к этой поверхности под действием сил притяжения их к молекулам твердого тела. Кроме того, какой бы поверхность ни была гладкой, она имеет выступы и впадины, в которых тормозятся молекулы движущейся жидкости. Прилипшие молекулы из-за вязкости жидкости взаимодействуют с текущими вблизи слоями жидкости, подтормаживая их. Теоретически такое тормозящее действие слоев друг на друга может простираться по направлению нормали к пластине в бесконечность, т.е. скорость вдоль нормали изменяется в таких пределах: при у=0 и~иw=0; при у=¥ и=ин, где иw - скорость на поверхности тела, ин - скорость невозмущенного потока.
Поэтому пограничный слой называется асимптотическим. Однако в большинстве интересующих нас случаев (маловязкие жидкости и большие скорости) значительное влияние прилипших молекул и, следовательно, существенное изменение скорости наблюдается только в относительно тонком пристеночном слое d/х<<1. Здесь d=f(х) – толщина пограничного слоя на расстоянии х от начала пластины, которая возрастает вдоль пластины, подтормаживая все новые слои жидкости. Вследствие асимптотичности пограничного слоя четкой границы его не существует. Условно принято, что внешняя граница пограничного слоя d соответствует такой ординате у, где скорость внутри пограничного слоя и составляет 99% от скорости в невозмущенном потоке ин, т.е.
| внутренняя граница y=0 и u=uw=0 внешняя граница y=d и u=0,99uн | (3.3) |
Всю область течения жидкости около твердого тела можно разбить на две зоны:
а) пограничный слой толщиной d(х). Это относительно тонкий слой d/х<<1, примыкающий к поверхности твердого тела. В этом слое существенно изменяется скорость от uw=0 до u=0,99uн и

Поэтому только внутри пограничного слоя проявляется вязкость жидкости и ее необходимо учитывать в расчетах;
б) набегающий невозмущенный поток и область, лежащая над пограничным слоем, в которых

Поэтому жидкость, текущую над пограничным слоем, можно считать идеальной (t=0) и анализировать ее движение по более простым законам течения идеальной жидкости. Теория пограничного слоя разделяет решение общей сложной задачи об обтекании тела потоком вязкой жидкости на две более простые: обтекание твердого тела лишь тонким слоем вязкой жидкости и обтекание твердого тела, несколько увеличенного в размерах на величину, пропорциональную толщине пограничного слоя, идеальной жидкостью.
Пограничный слой возникает при всех реальных течениях в лопаточных машинах, входных устройствах, соплах и существенно влияет на их работу. Теория пограничного слоя позволяет сознательно управлять этими течениями, а также рассчитывать их.
| Сжимаемость – это свойство жидкостей изменять плотность (объем) при изменении давления и температуры. |
Для количественной оценки сжимаемости используется модуль упругости жидкостей к Модуль упругости есть отношение изменения давления DР к относительному изменению плотности Dr/r.
Таким образом,

| (3.4) |
Относительное изменение плотности при заданном изменении давления

обратно пропорционально модулю упругости к. Капельные жидкости мало сжимаемые, и их модули упругости достаточно велики. Соответственно сжимаемость таких жидкостей очень мала. Численные значения модулей упругости некоторых жидкостей приведены в таблице 3.1.
Таблица 3.1
| Вещество | Вода | Керосин | Ртуть |
| к, Па | 2∙109 | 1,3∙109 | 3,3∙109 |
При изменении температуры плотность жидкости изменяется более существенно. Это свойство используется в термометрах и термостатах. Сжимаемость газов очень велика. Переходя от конечных разностей к дифференциалам, получим

| (3.5) |
Для изоэнтропического процесса РVк=соnst.
Так как r=1/V, то P=rк соnst.
Прологарифмируем последнее выражение
lnP=кlnr+lnconst
Продифференцируем полученное выражение

Окончательно получим соотношение

| (3.7) |
Скорость звука а - это скорость распространения малых возмущений давления в данной среде. Скорость звука определяется по формуле

| (3.8) |
Вывод этой формулы будет дан в дальнейшем. С учетом (1.7) можно записать

| (3.9) |
Используя уравнение состояния (3.1), также получим

| (3.10) |
В несжимаемых средах r=const, dр=0 и а=∞ т.е. возмущения распространяются мгновенно. Все жидкости в большей или меньшей степени сжимаемы, и звук в них распространяется с конечной скоростью. Скорость звука в данном газе (к=const, R=const) зависит от его абсолютной температуры (1.10). Скорость звука в различных газах при одинаковой температуре зависит от их природы (к=var, R=var). Показатель адиабаты для различных газов изменяется в узких пределах (1,1¼1,67), поэтому основное влияние оказывает газовая постоянная (см. табл. 3.2).
На практике вместо абсолютной скорости потока газа w удобно пользоваться числом Маха, которое равно отношению абсолютной скорости потока газа к местной скорости звука

Скорость распространения звука а связана с модулем упругости газа к.
По определению

В то же время
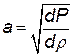
Следовательно, можем получить к=ra2 или

| (3.11) |
Таблица 3.2
| Газ | Показатель адиабаты | Газовая постоянная R., Дж/кг К | Скорость звука а, м/с |
| Фреон | 1,14 | 8,7¦T1/2 | |
| Воздух | 1,4 | 20,1¦T1/2 | |
| Гелий | 1,61 | 58,9¦T1/2 | |
| Водород | 1,4 | 76,4¦T1/2 |
Таким образом, число Маха в газовой динамике является важнейшим критерием сжимаемости движущегося газа. Обычно считают, что при М<0.3 газ можно рассматривать как несжимаемую жидкость. Для воздуха при нормальной температуре (Т=293К) это соответствует скорости 100 м/с, т.е., если поток воздуха движется со скоростью менее 100 м/с, его можно считать несжимаемой жидкостью и рассчитывать по формулам, считая р=const.
Дата добавления: 2015-04-18; просмотров: 335; Мы поможем в написании вашей работы!; Нарушение авторских прав |