Уравнение неразрывности (расхода) жидкости

Основные уравнения газовой динамики мы выведем для элементарной (единичной) струйки газа, поперечные размеры которой настолько малы, что в каждом ее сечении можно считать постоянными все основные параметры потока: скорость, давление, температуру и плотность газа.

Будем рассматривать стационарное (установившееся) движение газа в элементарной струйке (рис. 3.3.), при котором в любой фиксированной точке пространства сохраняются неизменными по времени скорость движения, давления, плотность и температура. Траектории частиц называются линиями тока. Боковая поверхность струйки является непроницаемой для жидкости или газа, так как векторы скорости движения касательны к ней. За бесконечно малый промежуток времени часть струйки 1 - 2 переместится в новое положение 1' - 2'.

Рис. 3.3. Элементарная струйка

Приток газа в объем 1' - 2 составит

где: r₁ - плотность в сечении 1;F₁ - площадь в сечении 1;

Расстояние dl₁ - между сечениями 1 и 1' равно

где w₁ - скорость в сечении 1; dt - элементарный промежуток времени.

В объем 1' - 2 поступает расход газа

Расход газа из объема 1' - 2 равен

При установившемся режиме течения приход газа равняется расходу

dМ₁=dМ₂=dМ.

Массовый расход газа в сечении 1 равен М₁=dМ₁/dt.

Соответственно в сечении 2: М₂=dМ₂/dt.

Так как М₂=М₁ окончательно получим уравнение расхода

для несжимаемой жидкости, т.е. при r=const, уравнение расхода примет вид

(3.12)

Из уравнения (3.12.) следует, что там, где площадь струйки больше, скорость меньше и наоборот. В местах сгущения линий тока скорость растет.е.сли линии тока раздвигаются, то скорость падает. В газе картина линий тока однозначно определяет изменение плотности тока.

который представляет собой массовый расход через единицу площади. В местах сгущения линий тока плотность тока увеличивается. Уравнение постоянства расхода можно представить также в дифференциальной форме

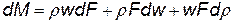
Разделив все члены этого соотношения на rwF, получим

(3.13)

Уравнение расхода можно использовать не для единичной струйки, а для трубопровода в целом. В этом случае под единичной струйкой понимается весь поток газа. В этом случае в каждом поперечном сечении считаются постоянными и равными средним значениям скорость, плотность, давление и температура.