
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос №27. Параллельное и последовательное соединение труб.
Последовательный трубопровод состоит из нескольких труб различной длины и различного диаметра, соединённых между собой.
Последовательное соединение трубопроводов. Рассмотрим трубопровод, состоящий из п последовательно соединенных труб различных диаметров. Каждый участок этого трубопровода имеет длину l и диаметр d.
В каждом из этих трубопроводов могут иметься свои местные сопротивления. Течение в жидкости в такой трубе подчиняется следующим условиям:
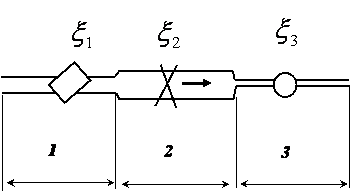 расход на всех участках трубопровода одинаков, т.е.
расход на всех участках трубопровода одинаков, т.е. 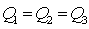 ;
;
потери давления (напора) во всём трубопроводе равны сумме потерь на каждом участке:
При движении жидкости по трубопроводу весь напор Н будет затрачен на преодоление потерь напора по длине.
Полная потеря напора в длинном трубопроводе равна сумме потерь на отдельных участках

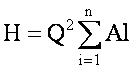
где l — длина участка, м; A— удельное сопротивление участка.
Для гидросистем:
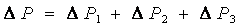 .
.
С учётом сказанного нетрудно получить уравнение для определения суммарных потерь давления, которое примет вид
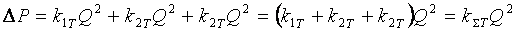 ,
,
где 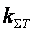 - суммарное гидравлическое сопротивление всего трубопровода.
- суммарное гидравлическое сопротивление всего трубопровода.
Величина суммарного сопротивления с учётом ранее полученной формулы для простых трубопроводов составит.
В общем случае выражение, описывающее суммарное гидравлическое сопротивление сложного трубопровода, будет выглядеть:
 .
.
Полученное уравнение, определяющее суммарные потери давления, представляет собой характеристику сложного трубопровода, которая являет  ся суммой характеристик простых трубопроводов. Это уравнение позволяет узнать, какие энергетические характеристики должен иметь источник энергии, чтобы жидкость могла протекать по всему трубопроводу. Однако в конечной точке этой трубы энергия жидкости будет равна нулю. Если в конце трубы необходимо иметь какое-то давление
ся суммой характеристик простых трубопроводов. Это уравнение позволяет узнать, какие энергетические характеристики должен иметь источник энергии, чтобы жидкость могла протекать по всему трубопроводу. Однако в конечной точке этой трубы энергия жидкости будет равна нулю. Если в конце трубы необходимо иметь какое-то давление 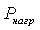 (например, чтобы преодолевать нагрузку) к величине
(например, чтобы преодолевать нагрузку) к величине 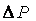 нужно добавить эту величину. Кроме того, т.к. в общем случае величина скоростного напора в начале
нужно добавить эту величину. Кроме того, т.к. в общем случае величина скоростного напора в начале 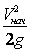 и в конце
и в конце 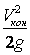 трубопровода из-за разных диаметров различны, необходимо добавить и эту разницу к
трубопровода из-за разных диаметров различны, необходимо добавить и эту разницу к 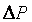 . В результате энергия, которой должен обладать источник, должна составлять
. В результате энергия, которой должен обладать источник, должна составлять
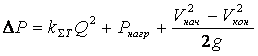 .
.
Отличительной особенностью таких трубопроводов является то, что поток жидкости делится в одной точке на несколько самостоятельных потоков, которые позже сходятся в другой точке. Каждый из этих потоков может содержать свои местные сопротивления. Наиболее часто возникающей задачей, связанной с расчётом таких трубопроводов, является определение расхода в каждой ветви. Рассмотрим движение жидкости по этим трубопроводам, считая, что потенциальная энергия положения 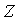 много меньше потенциальной энергии сжатия, которая определяется давлением, и ею можно пренебречь. Если считать, что в местах разветвления и соединения трубопроводов, обозначенных буквами н и к, расход
много меньше потенциальной энергии сжатия, которая определяется давлением, и ею можно пренебречь. Если считать, что в местах разветвления и соединения трубопроводов, обозначенных буквами н и к, расход 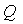 одинаков, а давления равны
одинаков, а давления равны 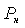 и
и 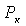 , то можно записать:
, то можно записать:

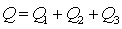
Особенность расчета заключается в том, что потери напора в каждой из линий одинаковы и равны разности напоров в узлах а и б.
h1= h2 = h3 = ... = hn = hA - hB=H
Расход через любую из линий, соединяющих точки А и В, может быть записан в виде
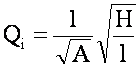
Так как сумма расходов во всех параллельных трубопроводах равна расходу Q до разветвления трубопровода
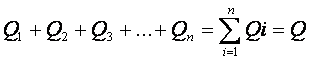
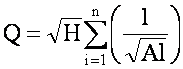
И для гидросистем
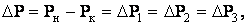
”P1, ”P2, ”P3– потери давления в соответствующих ветвях.
Представляя каждую из параллельных ветвей как простой трубопровод, можно записать характеристики каждой ветви:
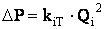

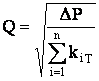
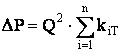

Из приведённых уравнений вытекает следующее важное правило: для построения характеристик параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик каждого из этих трубопроводов при одинаковых ординатах (потерях давления).
Вопрос №28. Трубопровод с равномерно распределённым путевым расходом.
Это такие трубопроводы, в которых вдоль всего пути расход
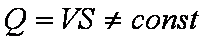
Расход в сечении А (рис.ы)
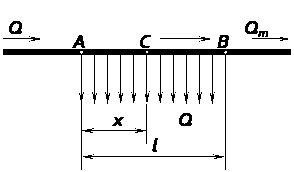
Схема к расчету трубопровода с путевым расходом
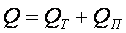
где QТ — транзитный расход; Qn — путевой расход.
Отношение путевого расхода Qn к длине трубопровода l называют удельным расходом q.
С течением времени расход постепенно уменьшается и становится равным QT в сечении В, а в произвольном сечении С расположенном на расстояниих от начального сечения А расход жидкости
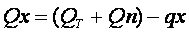
Потери напора по длине в трубопроводе для квадратичной области турбулентного режима
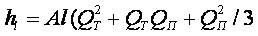
Если на участке АВ будет отобран весь расход, т. е. отсутствует транзитный расход (QT = 0), то потери напора по длине в данном частном случае примут вид формулы, которая носит название формулы Дюпуи:
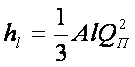
В случае расчета трубопроводов с путевым расходом с достаточной степенью точности Qп2 /3 можно заменить членом Qп2 /4. Тогда
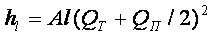
Расчетный расход на участке АВ
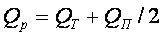
Анализ этой формулы показывает, что путевой расход Qп эквивалентен транзитному расходу и зависит от степени равномерности отбора жидкости по длине трубопровода.
Расчет кольцевой сети. Кольцевая сеть состоит из замкнутых колец и магистралей, присоединенных к водонапорной башне или резервуару. Рассмотрим простейший случай расчета кольцевой водопроводной сети, состоящей из магистрального трубопровода А—В и одного кольца В—1—2—3—-4—В (рис. ). Расход, забираемый в точках 1, 2, 3, 4, обозначим соответственно через Q1, Q2, Q3, Q4
На основании топографических данных, длины участков трубопровода, диаметра труб задаемся направлением движения воды по кольцу и нулевой (раз
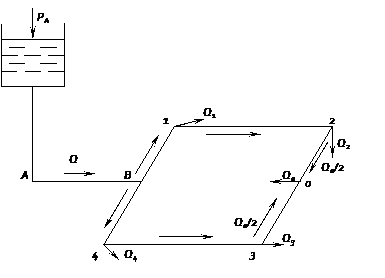
дельной) точкой сети. Нулевая точка выбирается таким образом, чтобы потери напора в ветвях слева и справа от этой точки были одинаковыми. Далее, так же как и при расчете тупиковой сети, определяем диаметр труб и подсчитываем потери напора на каждом участке по левой и правой сторонам кольца.
Если нулевая точка О выбрана правильно, то сумма потерь напора по левой стороне кольца должна равняться сумме потерь напора по правой стороне кольца, т. е.
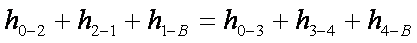
где h0-2 и т.д. - потери напора по длине на соответствующем участке
Если это условие не выполняется, то расчет следует продолжать до тех пор, пока не будет получено равенство потерь напора в двух рассматриваемых разомкнутых сетях.
Вопрос №29. Расчет сложного трубопровода.
К сложным трубопроводам следует относить те трубопроводы, которые не подходят к категории простых трубопроводов, т.е к сложным трубопроводам следует отнести:
трубопроводы, собранные из труб разного диаметра (последовательное соединение трубопроводов),
трубопроводы, имеющие разветвления: параллельное соединение трубопроводов, сети трубопроводов, трубопроводы с непрерывной раздачей жидкости.
Последовательное соединение трубопроводов. При последовательном соединении
трубопроводов конец предыдущего простого трубопровода одновременно является началом следующего простого трубопровода. В сложном трубопроводе, состоящем из последовательно соединённых простых 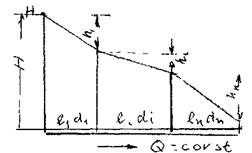 трубопроводов, последние в литературе называются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопроводе будут равны сумме потерь напора во всех отдельных его участках.
трубопроводов, последние в литературе называются участками этого трубопровода. Расход жидкости во всех участках сложного трубопровода остаётся одинаковым Q = const. Общие потери напора во всём трубопроводе будут равны сумме потерь напора во всех отдельных его участках.
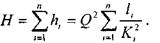
 где
где 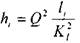 - потери напора на
- потери напора на 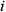 - том участке трубопровода.
- том участке трубопровода.
Таким образом, потери напора в трубопроводе, состоящем из последовательно соединённых друг с другом участков равны квадрату расхода жидкости в трубопроводе умноженному на сумму удельных сопротивлений всех участков.
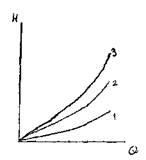
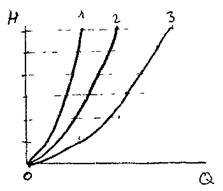
Гидравлическая характеристика трубопровода состоящего из последовательно соединённых участков представляет собой графическую сумму (по оси напоров) гидравлических характеристик всех отдельных участков. На рисунке кривая 1 представляет гидравлическую характеристику 1-го участка трубопровода, кривая 2 - гидравлическую характеристику 2-го участка, кривая 3 - сумму гидравлических характеристик обеих участков.
Сложный трубопровод, состоящий из последовательно соединённых простых трубопроводов можно свести к простому трубопроводу с одинаковым (эквивалентным) диаметром, при этом длины участков будут пересчитываться, чтобы сохранить реальные гидравлические сопротивления участков трубопровода.
Так приведённая длина 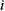 - того участка
- того участка 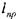 будет:
будет:
'Л 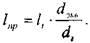
Следует отметить, что величина скоростного напора также зависит от диаметра трубопровода, и при определении приведённой длины участка мы вносим некоторуюошибку, которая будет тем большей, чем больше разница в величинах фактического и эквивалентного диаметров. В таких случаях можно рекомендовать другой, более сложный способ.
Параллельное соединение трубопроводов. Схема прокладки параллельных трубопроводов используется в тех случаях, когда на трассе магистрального трубопровода естьучастки, где требуется уменьшить гидравлические сопротивления трубопровода (высокие перевальные точки трубопровода) или при заложении трубопровода в трудно доступных местах (переход через реки и др.). При параллельном соединении трубопроводов имеются две особые точки, называемые точками разветвления.
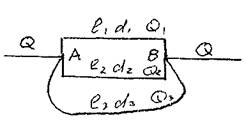
В этих точках находятся концы параллельных ветвей трубопровода (точки А и В). Будем считать, что жидкость движется слева направо, тогда общий для всех ветвей напор в точке А будет больше напора в другой общей для всех ветвей трубопровода точке В (НА  Н к ). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в единый трубопровод. Каждая ветвь может иметь различные геометрические размеры: диаметр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е.
Н к ). В точке А поток жидкости растекается по параллельным ветвям, а в точке В вновь собирается в единый трубопровод. Каждая ветвь может иметь различные геометрические размеры: диаметр и протяжённость (длину). Поскольку вся система трубопроводов является закрытой, то поток жидкости в данной системе будет транзитным, т.е.
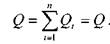
Жидкость движется по всем ветвям при одинаковой разности напоров:
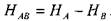 > тогда расход жидкости по каждой ветви можно записать в виде:
> тогда расход жидкости по каждой ветви можно записать в виде:
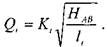
Поскольку ветвей в системе п,, а число неизвестных в системе уравнений будет п+1, включая напор, затрачиваемый на прохождение жидкости по всем ветвям 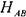 , то в качестве дополнительного уравнения в системе будет использовано уравнение неразрывности:
, то в качестве дополнительного уравнения в системе будет использовано уравнение неразрывности:
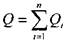
При решении системы уравнений можно воспользоваться соотношением:
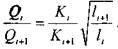
Для построения гидравлической характеристики системы параллельных трубопроводов можно воспользоваться методом графического суммирования. Суммирование осуществляется по оси расходовQ. т.к. 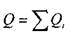
Трубопроводы с непрерывным (распределённым расходом). В данном случае предполагается, что вдоль всей длины трубопровода располагаются одинаковые равномернораспределённые потребители жидкости. Классическим примером такого трубопровода может служить оросительная система. В начальной точке трубопровода напор составляет Н. В общем случае, расход по трубопроводу состоит из транзитного Qm и
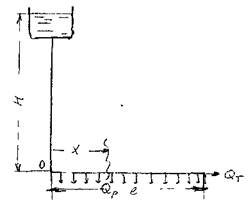
расхода Qp ,который непрерывно раз даётся по всей длине трубопровода.
Тогда в некотором сечении трубопровода на расстоянии х от его начала расход будет равен:
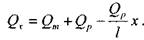
Тогда гидравлический уклон в сечении х на малом отрезке dx:
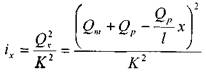
Уравнение падения напора вдоль элемента dx запишется следующим образом:
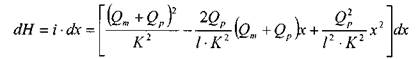
После интегрирования от 0 до / получим:
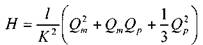
и при 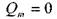 :
: 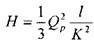
Сети трубопроводов. Если магистральные трубопроводы принято рассматривать как средства внешнего транспорта жидкостей и газов, то сети используются в качестве оборудования для внутреннего транспорта жидких или газообразных продуктов. По направлению движения жидкости (газа) сети различают на сборные и раздаточные (распределительные). В сборных сетях имеется группа источников возникновения  жидкости (газа). Жидкость от этих источников направляется в своеобразные узлы сбора и оттуда - в магистральный трубопровод. Классическим примером сборной сети может служить нефтесборная система со скважин, канализационная сеть. В раздаточных (распределительных) сетях жидкость или газ поступает из магистрального трубопровода и по сети распределяется по потребителям (абонентам). Распространённым примером
жидкости (газа). Жидкость от этих источников направляется в своеобразные узлы сбора и оттуда - в магистральный трубопровод. Классическим примером сборной сети может служить нефтесборная система со скважин, канализационная сеть. В раздаточных (распределительных) сетях жидкость или газ поступает из магистрального трубопровода и по сети распределяется по потребителям (абонентам). Распространённым примером  распределительной сети является система водоснабжения. К такому же типу сетей можно также отнести систему принудительной вентиляции,
распределительной сети является система водоснабжения. К такому же типу сетей можно также отнести систему принудительной вентиляции,
где воздух подаётся в служебные помещения или на рабочие места. К такому же типу сетей можно отнести систему теплоснабжения и др. Сети строятся в населённых пунктах, на предприятиях, отдельных территориях. Трубы в таких системах могут изготавливаться из различных материалов в зависимости от технологических требований, предъявляемых к сетям. В сборных сетях источники жидкости и газа располагают напором, обеспечивающим движение жидкости (газа) до магистралей. Если напоры недостаточны, то создаются специальные, узлы, где напор обеспечивается принудительным образом. Имеется, по крайней мере, две группы задач для гидравлического расчёта сетей: проектирование новых сетей и расчёт пропускной способности существующих сетей. Принципы расчёта похожи. В основе расчётных формул положены уравнения Дарси-Вейсбаха и Шези. Предварительно в сети выбирается ветвь с наибольшей нагрузкой (расход и напор). Эта ветвь рассматривается как своеобразный трубопровод, который, в общем случае можно отнести к категории последовательного соединения простых трубопроводов. Другие участки рассчитываются самостоятельно. После завершения расчётных работ, осуществляется проверка соответствия результатов расчётов в узлах сети. После анализа расхождений результатов решений в узлах сети осуществляется корректировка исходных данных. Таким образом, метод итераций является наиболее приемлемым для расчёта сетей.
Трубопроводы некруглого профиля. Подавляющее большинство трубопроводов собирается из круглых труб. Преимущество круглого сечения очевидны: круглое сечение обладает максимальной пропускной способностью и минимальным гидравлическим сопротивлением. Так гидравлический радиус для круглого сечения: 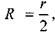
для треугольного сечения 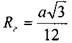 для квадратного сечения
для квадратного сечения 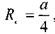
для шестиугольного сечения 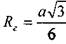
Тем не менее, трубы некруглого сечения применяются в промышленности там, где потери напора не играют особой роли. Это, в первую очередь, воздуховоды с малыми скоростями движения воздуха, и т.д.
Трубопроводы, работающие под вакуумом (сифоны). Сифоном называется такой самотёчный трубопровод, часть которого располагается выше уровня жидкости в резервуаре. Действующий напор представляет собой разницу уровней в резервуарах Az. Для приведения сифона в действие необходимо предварительно откачать из сифона воздух и создать в нём разряжение. При этом жидкость поднимется из резервуара А до верхней точки сифона, после чего жидкость начнёт двигаться по ниспадающей части трубопровод в резервуар В. Другой метод 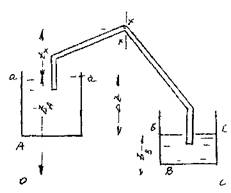 xзапуска сифона - заполнить его жидкостью извне. Запишем уравнение Бернулли для двух сечений а-а и b-b относительно плоскости сравнения О - О.
xзапуска сифона - заполнить его жидкостью извне. Запишем уравнение Бернулли для двух сечений а-а и b-b относительно плоскости сравнения О - О.
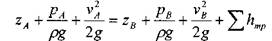
Поскольку:  , то:
, то:
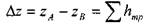 ?
?
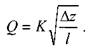
Критическим сечением в сифоне будет сечение х - х в верхней точке сифона. Давление в этой точке будет минимальным и для нормальной работы сифона необходимо, чтобы оно выло выше упругости паров перекачиваемой по сифону жидкости.
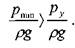
Дата добавления: 2015-04-18; просмотров: 149930; Мы поможем в написании вашей работы!; Нарушение авторских прав |