Вопрос №21. Гидравлические сопротивления. Формулы Дарси-Вейсбаха.

Гидравлическая жидкость в гидросистемах технологического оборудования, как уже обсуждалось ранее, играет роль рабочего тела. Она обеспечивает перенос энергии от источника гидравлической энергии к потребителю (в большинстве случаев, к гидродвигателю). Для такого переноса используются напорные потоки. В подобных потоках жидкость со всех сторон ограничена твёрдыми стенками трубопроводов, каналов гидроаппаратов и полостей гидромашин. В дальнейшем мы будем ориентироваться именно на такие случаи, хотя аналогичные процессы сопровождают и движение безнапорных потоков.

Естественно, что твёрдые стенки препятствуют свободному движению жидкости. Поэтому при относительном движении жидкости и твердых поверхностей неизбежно возникают (развиваются) гидравлические сопротивления. На преодоление возникающих сопротивлений затрачивается часть энергии потока. Эту потерянную энергию называют гидравлическими потерями удельной энергии или потерями напора. Гидравлические потери главным образом связаны с преодолением сил трения в потоке и о твёрдые стенки и зависят от ряда факторов, основными из которых являются:

геометрическая форма потока,

размеры потока,

шероховатость твёрдых стенок потока,

скорость течения жидкости,

режим движения жидкости (который связан со скоростью, но учитывает её не только количественно, но и качественно),

вязкость жидкости,

некоторые другие эксплуатационные свойства жидкости.

Ногидравлические потери практически не зависят от давления в жидкости.

Величина гидравлических потерь оценивается энергией, потерянной каждой весовой единицей жидкости. Из уравнения Бернулли, составленного для двух сечений потока, обозначенных индексами 1 и 2 потери энергии потока жидкости можно представить как

Потери напора по длине, иначе их называют потерями напора на трение, в чистом виде, т.е. так, что нет никаких других потерь, возникают в гладких прямых трубах с постоянным сечением при равномерном течении. Такие потери обусловлены внутренним трением в жидкости и поэтому происходят и в шероховатых трубах, и в гладких. Величина этих потерь выражается зависимостью

,

где - коэффициент сопротивления, обусловленный трением по длине.

При равномерном движении жидкости на участке трубопровода постоянного диаметра d длиной l этот коэффициент сопротивления прямо пропорционален длине и обратно пропорционален диаметру трубы

,

где l– коэффициент гидравлического трения (иначе его называют коэффициент потерь на трение или коэффициент сопротивления трения).

Из этого выражения нетрудно видеть, что значение l - коэффициент трения участка круглой трубы, длина которого равна её диаметру.

С учетом последнего выражения для коэффициента сопротивления потери напора по длине выражаются формулой Дарси

.

Эту формулу можно применять не только для цилиндрических трубопроводов, но тогда надо выразить диаметр трубопровода d через гидравлический радиус потока

или

где, напомним, Й – площадь живого сечения потока,

З - смоченный периметр.

Гидравлический радиус можно вычислить для потока с любой формой сечения, и тогда формула Дарси принимает вид

.

Эта формула справедлива как для ламинарного, так и для турбулентного режимов движения жидкости, однако коэффициент трения по длине »не является величиной постоянной.

Для определения физического смысла коэффициента »рассмотрим объём жидкости длиной l, который равномерно движется в трубе диаметром d со скоростьюV. На этот объём действуют силы давления P1 и P2, причём P1> P2, и силы трения рассматриваемого объёма о стенки трубы, которые определяются напряжением трения на стенке трубы Д0. Условием равномерного движения под действием сказанных сил будет следующее равенство:

.

Если учесть, что

, ^то ,

и подставить эту величину в уравнение сил, действующих на рассматриваемый объём, получим:

.

Сократив последнее выражение, получим . Выразив из него », окончательно будем иметь

.

Местными гидравлическими сопротивлениями называются любые участки гидравлической системы, где имеются повороты, преграды на пути потока рабочей жидкости, расширения или сужения, вызывающие внезапное изменение формы потока, скорости или направления ее движения. В этих местах интенсивно теряется напор. Примерами местных сопротивлений могут быть искривления оси трубопровода, изменения проходных сечений любых гидравлических аппаратов, стыки трубопроводов и т.п. Потери напора на местных сопротивлениях определяются по формуле Вейсбаха:

;

где - коэффициент местного сопротивления.

Коэффициент местного сопротивления зависит от конкретных геометрических размеров местного сопротивления и его формы. В связи со сложностью процессов, которые происходят при движении жидкости через местные сопротивления, в большинстве случаев его приходится определять на основании экспериментальных данных.

Однако в некоторых случаях величины коэффициентов местных сопротивлений можно определить аналитически.

Из определения коэффициента видно, что он учитывает все виды потерь энергии потока жидкости на участке местного сопротивления. Его физический смысл состоит в том, что он показывает долю скоростного напора, затрачиваемого на преодоление данного сопротивления.

Коэффициенты различных сопротивлений можно найти в гидравлических справочниках. В том случае, если местные сопротивления находятся на расстоянии меньше (25ч50)d друг от друга ( - диаметр трубопровода, соединяющего местные сопротивления), весьма вероятно их взаимное влияние друг на друга, а их действительные коэффициенты местных сопротивлений будут отличаться от табличных. Такие сопротивления нужно рассматривать как единое сложное сопротивление, коэффициент которого определяется только экспериментально. Нужно отметить, что из-за взаимного влияния местных сопротивлений, расположенных вблизи друг друга в потоке, во многих случаях суммарная потеря напора не равна простой сумме потерь напора на каждом из этих сопротивлений.

Это трубопроводы постоянного по длине диаметра, у которых основными являются потери напора по длине, а местными потерями напора и скоростным напором можно пренебречь.

Потери напора по длине трубопровода определяютпо формуле Дарси—Вейсбаха:

Учитывая, что расход Q = VЧS и скорость движения потока тогда

или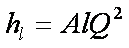

где А — удельное сопротивление трубопровода, определяемое по справочным таблицам;

Для переходной области удельное сопротивление Ао=А*b,

где b — поправочный коэффициент, учитывающий зависимость коэффициента гидравлического трения l от числа Рейнольдса.

Кроме удельного сопротивления А в литературе по гидравлике для решения задач приводится способ расчета длинных трубопроводов, базирующийся на формуле Шези.

Широко применяемые гидравлические параметры — это модуль расхода , сопротивление трубопровода ST=A*l, проводимость трубопровода . С помощью вышеуказанных параметров потери напора по длине можно определить следующим образом: