Вопрос №20. Основное уравнение равномерного движения жидкости. Формула Шези.

Рассмотрим прямолинейное равномерное движение жидкости. Живые сечения в этом случае могут быть произвольной формы, но не должны изменяться по всей длине рассматриваемого участка. В таком потоке потери напора определяются лишь потерями по длине.

Выделим из потока участок жидкости длиной l и запишем уравнение Бернулли для сечений 1 и 2( рис. 32 )

Рис. 38

где

z1 , z2 - ординаты центра тяжести сечений 1,2,

p1 , p2 - давление в центрах тяжести этих сечений,

v1 , v2 - средние скорости в этих сечениях,

h1-2 - потери напора по длине.

Так как движение равномерное, то v1 =v2 и уравнение можно переписать так:

. (1)

В случае равномерного движения разность удельных потенциальных энергий равна потере напора по длине.

Для вычисления этой разности напишем сумму проекций на ось А-А всех сил, действующих на участке 1-2. Эти силы следующие:

1) сила тяжести жидкости

,

2) силы давления на плоские сечения

, , ,

3) сила трения

,

где t - сила трения на единицу площади смачиваемой поверхности

русла, c - смоченный периметр,

4) силы давления стенок на жидкость ( эти силы не подсчитываем, так как они параллельны оси А-Аи, следовательно, их проекции на ось А-А равны нулю ).

Спроектируем все эти силы на ось А-А:

.

Из рисунка

.

Подставим выражение для сил в уравнение

.

Разделим обе части этого равенства на , имеем

. (2)

Сравнивая выражения (1) и (2), находим

,

откуда

.

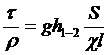Отношение площади живого сечения S к смоченному периметру c называется гидравлическим радиусом

.

Величина обозначается через i и называется гидравлическим уклоном.

Получаем

.

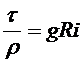Это уравнение называется основным уравнением равномерного движения.

Величина имеет размерность квадрата скорости

.

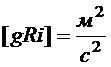Выражение - называется динамической скоростью, обозначается v*

.

Формула Шези — формула для определения средней скорости потока при установившемся равномерном турбулентном движении жидкости в области квадратичного сопротивления для случая безнапорного потока. Опубликована французским инженером-гидравликом А. Шези (AntoinedeChézy, 1718–1798) в 1769 году. Применяется для расчётов потоков в речных руслах и канализационых системах.

,

где V — средняя скорость потока, м/с;

C — коэффициент сопротивления трения по длине (коэффициент Шези), являющийся интегральной характеристикой сил сопротивления;

R — гидравлический радиус, м;

I — гидравлический уклон м/м.

Формула Шези имеет то же предназначение, что и формула Дарси-Вейсбаха. Коэффициент потерь на трение связан с коэффициентом сопротивления С следующей зависимостью:

.

Коэффициент сопротивления C может быть определён по формуле Н. Н. Павловского:

где n — коэффициент шероховатости, характеризующий состояние поверхности русла, для случая канализационных труб принимается в диапазоне (0,012...0,015); для других случаев nbsp;— информация приведена в литературе^[1]

у — показатель степени, зависящий от величины коэффициента шероховатости и гидравлического радиуса:

Эта формула рекомендуется для значений R < (3...5)м. При больших гидравлических радиусах или других значениях коэффициентов шероховатости применение формулы Н. Н. Павловского в гидравлических расчётах речных русел приводит к значительным ошибкам.

При значении y = 1/6 формула Шези приводится к формуле Маннинга.

Существуют и другие эмпирические формулы для определения коэффициента сопротивления C^[2]