
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос №22. Гидравлический коэффициент трения, его зависимость и определение
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис.4.3).

Рис. 4.3. Схема для рассмотрения ламинарного потока
Уравнение, связывающее переменные υ и r, имеет следующий вид:
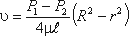
где P1 и P2 - давления соответственно в сечениях 1 и 2.
У стенок трубы величина r = R, , значит скорость υ = 0, а при r = 0 (на оси потока) скорость будет максимальной

Теперь определим расход жидкости при ламинарном течении в круглой трубе. Так как эпюра распределения скоростей в круглой трубе имеет вид параболоида вращения с максимальным значением скорости в центре трубы, то расход жидкости численно равен объему этого параболоида. Определим этот объем.
Максимальная скорость дает высоту параболоида

Как известно из геометрии, объем параболоида высотой h и площадью ρR2 равен

а в нашем случае

Если вместо R подставить диаметр трубы d, то формула (4.4) приобретет вид

Расход в трубе можно выразить через среднюю скорость:
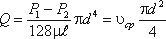
откуда

Для определения потерь напора при ламинарном течении жидкости в круглой трубе рассмотрим участок трубы длиной l, по которому поток течет в условиях ламинарного режима (рис.4.3).
Потеря давления в трубопроводе будет равна

Если в формуле динамический коэффициент вязкости μ заменить через кинематический коэффициент вязкости υ и плотность ρ ( μ = υ ρ ) и разделить обе части равенства на объемный вес жидкости γ = ρ g, то получим:

Так как левая часть полученного равенства равна потерям напора hпот в трубе постоянного диаметра, то окончательно это равенство примет вид:

Уравнение может быть преобразовано в универсальную формулу Вейсбаха-Дарси, которая окончательно записывается так:
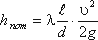
где λ - коэффициент гидравлического трения, который для ламинарного потока вычисляется по выражению:

Однако при ламинарном режиме для определения коэффициента гидравлического трения λ Т.М. Башта рекомендует при Re< 2300 применять формулу
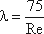
Дата добавления: 2015-04-18; просмотров: 450; Мы поможем в написании вашей работы!; Нарушение авторских прав |