Вопрос №14 Струйная модель движения жидкости, параметры потока.

В гидравлике рассматривается струйная модель движения жидкости, т.е. поток представляется как совокупность элементарных струек жидкости, имеющих различные скорости течения us. Индекс Sозначает (напоминает), что в каждой точке живого сечения скорости различны. Элементарные струйки как бы скользят друг по другу. Они трутся между собой и вследствие этого их скорости различаются. Причём, в середине потока скорости наибольшие, а к периферии они уменьшаются. Распределение скоростей по живому сечению потока можно представить в виде параболоида с основанием, равным S. Высота его в любой точке равна скорости соответствующей элементарной струйки uS. Площадь элементарной струйки равна dS. В пределах этой площади скорость можно считать постоянной. Понятно, что за единицу времени через живое сечение потока будет проходить объём жидкости Vt, равный объёму параболоида. Этот объём жидкости и будет равен расходу потока.

.

С учётом понятия средней скорости, которая во всех точках живого сечения одинакова, за единицу времени через живое сечение потока будет проходить объём жидкости (обозначим его Vtср ), равный:

Vtср=SVср.

Если приравнять эти объёмы Vtср = Vt=параболоида, можно определить значение средней скорости потока жидкости:

В дальнейшем среднюю скорость потока жидкости будем обозначать буквой V без индекса ср.

При неравномерном движении средняя скорость в различных живых сечениях по длине потока различна. При равномерном движении средняя скорость по длине потока постоянна во всех живых сечениях.

Вопрос №15. Уравнение неразрывности потока.

Рассмотрим установившийся поток между живыми сечениями 1,2 ( рис. 26 ).

Рис. 26

Живым сечением называется поверхность в пределах потока, проведенная параллельно к направлению струек. За единицу времени через живое сечение 1 в рассматриваемый объем жидкости ,

где 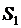- площадь живого сечения, - средняя скорость в сечении.

Через живое сечение 2 за это время вытекает объем жидкости

,

где - площадь живого сечения 2, 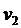- средняя скорость в сечении 2.

Поскольку форма объема 1-2 с течением времени не изменяется, жидкость несжимаемая, объем жидкости должен равняться объему вытекающему .

Поэтому можно записать

.

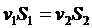Это уравнение называется уравнением неразрывности.

Из уравнения неразрывности следует, что

.

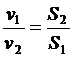Средние скорости обратно пропорциональны площадям соответствующих сечений.

Вывод основных гидродинамических уравнений начнём с вывода уравнения неразрывности, выражающего закон сохранения в гидродинамике.

Математическое описание состояния движущейся жидкости осуществляется с помощью функций, определяющих распределение скоростей и каких-либо двух термодинамических величин, например, 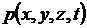- давления и - плотности.

Скорость, давление и плотность жидкости будем относить к данным точкам пространства, а не к определённым частицам жидкости, передвигающимся во времени и в пространстве. То есть будем пользоваться переменными Эйлера.

Рис. 11

Рассмотрим некоторый объём Vo пространства. Количество (масса) жидкости в этом объёме есть . Через элемент поверхности 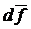, ограничивающей рассматриваемый объём, в единицу времени протекает количество жидкости ( рис. 11).

Вектор 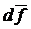по абсолютной величине равен площади элемента поверхности и направлен по внешней нормали к ней. Тогда положительно, если жидкость вытекает из объёма, и отрицательно, если жидкость втекает в него.

Полное количество жидкости, вытекающей в единицу времени из объёма Vo

.

где S - поверхность, ограничивающая выделенный объём Vo.

С другой стороны, уменьшение количества жидкости в объёме Vo можно записать в виде

.

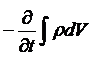Приравнивая оба выражения, получаем:

.

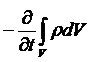
Интеграл по поверхности преобразуем в интеграл по объёму

.

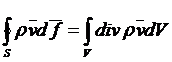Таким образом,

.

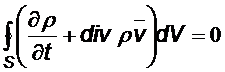Поскольку это равенство должно иметь место для любого выделенного объёма, то должно быть равным нулю подынтегральное выражение, т.е.

.

Получили уравнение неразрывности.

Расписав выражение 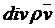можно записать

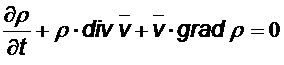
В декартовых координатах

.

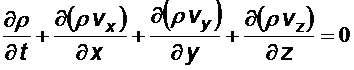Вектор называют плотностью потока жидкости.

Его направление совпадает с направлением движения жидкости, а абсолютная величина определяет количество жидкости, протекающей в единице времени через единицу площади, расположенной перпендикулярно к скорости.