Вопрос №11. Относительное равновесие жидкости в сосуде, равномерно вращающемся вокруг вертикальной оси.

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω²r, где r - расстояние частицы от оси вращения, а ω - угловая скорость вращения сосуда.

Рис. 2.7. Вращение сосуда с жидкостью

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

С другой стороны:

где z - координата рассматриваемой точки. Таким образом, получаем:

откуда

или после интегрирования

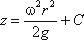
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь

т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.

Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь

После сокращений получим

Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.

Вопрос №12. Поверхности равных давлений. Гидростатический закон распределения давления.

Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции.

Найдем величину равного давления Р по трем частным производным. При Р=const и р # 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид

Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающиеся случаи.

Первый случай,когда на покоящуюся жидкость действует одна внешняя сила, сила тяжести, тогда , , (направление ускорения свободного падения не совпадает с положительным направлением оси Z). В этом случае исходное уравнение имеет вид

или

т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Zсоответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоскостей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.

Сначала рассмотрим простейший случай покоя. Жидкость находится под действием силы тяжести. Это означает, что проекции ускорений на оси X и Y отсутствуют. Единственным ускорением является ускорение свободного падения g, т. е.:

, , .

Тогда полный дифференциал давления после подстановки в него ускорений примет вид:

.

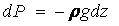После интегрирования этого выражения получим:

.

Постоянную интегрирования, равную

^,

найдём, подставив параметры свободной поверхности и .

После подстановки этих значений в интеграл P будем иметь равенство:

Переписав это выражение в другом виде, получим

Если обозначить (Z0 - Z) через h, то приведённое равенство примет уже знакомый вид основного уравнения гидростатики

.

Из этого же равенства можно получить следующий вид

,

или

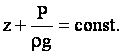
Последнее выражение часто называют основным законом гидростатики.

Вопрос №13. Виды движения жидкости. Измерение расхода жидкости, приборы

Проведём классификацию видов движения жидкости.

1. Классификация по признаку зависимости движения жидкости от времени.

1.1. Установившееся (стационарное).

1.2. Неустановившееся (нестационарное).

2. Классификация по признаку учёта сил трения, вязкости и теплопроводности.

2.1. Идеальная невязкая жидкость.

2.2. Вязкая жидкость.

3. Классификация по виду движения жидкости (поступательное или вращательного движение).

3.1. Безвихревое (потенциальное) (движение, когда вращение отсутствует).

3.2. Вихревое движение.

4. Классификация по характеру изменения плотности в потоке.

4.1. Несжимаемая (жидкость), r=const.

4.2. Сжимаемая (газ), r¹const.

5. Классификация по скорости и её отношению к скорости

расширяющихся возмущений (скорости звука).

5.1. Дозвуковое ( M<1) , где , V - скорость потока, а – скорость звука.

5.2. Трансзвуковое (М»1).

5.3. Сверхзвуковое (М>1).

5.4. Гиперзвуковое (М>>1).

6. Классификация по режиму течения.

6.1. Ламинарный режим, (Re£Reкр).

6.2. Турбулентный режим,(Re/Reкр).

7. Вид течения.

7.1. Свободное.

7.2. Вынужденное.