Вопрос № 23. Уравнение Бернулли для реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

= h_лин + h_мест

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ, g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго сечения используют уравнение постоянства расхода жидкости υ₁ω ₁ = υ₂ω₂.

Вопрос №24. Водомер Вентури (вывод формулы расхода жидкости).

Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и II-II:

или

Используя уравнение неразрывности

Q = υ₁ω₁ = υ₂ω₂

сделаем замену в получено выражении:

Решая относительно Q, получим

Выражение, стоящее перед , является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Вопрос №25. Гидравлический расчет коротких трубопроводов.

Рассмотрим короткий трубопровод с местным сопротивлением, присоединенным к резервуару, заполненному жидкостью. Истечение жидкости в атмосферу из трубопровода длиной l и диаметром dпроисходит под постоянным напором H (рис. 49).

Рис. 49

При заданных длине l и диаметре трубопровода d необходимо определить скорость движения жидкости v и расход Q.

Составим уравнение Бернулли для сечений 1 и 2. При этом считаем, что и .

или

,

где hw - суммарные (местные и по длине) потери напора между сечениями 1 и 2, которые можно представить в виде зависимости

,

где

.

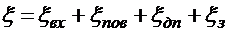Формулу можно записать в следующем виде

.

Отсюда найдем скорость истечения

,

где j - коэффициент скорости.

Расход, пропускаемый коротким трубопроводом

.

Вопрос №26 Гидравлический расчет длинных трубопроводов.

Рассмотрим трубопровод, состоящий из последовательно соединенных длинных труб разного диаметра d1,…, dn и длины l1,…, ln при постоянном расходе жидкости по длине трубопровода (рис. 50).

Рис. 50

Расчет сводится к определению суммарных потерь напора по длине трубопровода, так как местными потерями пренебрегают

.

Преобразуем выражение для потери напора по длине

,

где - расходная характеристика.

Тогда

.

Формула показывает, что трубопровод, составленный из последовательно соединенных труб разного диаметра и длины, можно рассматривать как простой трубопровод, суммарные потери напора, в котором равны сумме потерь напора составляющих его труб.

Формула позволяет решить и обратную задачу, т.е. при заданных напоре, диаметре труб вычислить расход Q :

.