Решение. 1. Составим уравнение Бернулли для уровней жидкости в резервуарах:

1. Составим уравнение Бернулли для уровней жидкости в резервуарах:

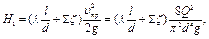
где υ_тр - средняя скорость жидкости в трубопроводе.

2. Жидкость маловязкая, вероятен турбулентный режим, поэтому значения ζ для фильтра, колена, задвижки и выхода из трубы опреде­ляем по прил. 2:

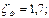
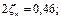
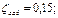
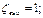
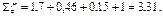
3. Решаем задачу графоаналитическим способом. Задаемся рядом

значений Q и определяем соответствующие им величины h_пот. Полученные данные приведены ниже.

Q, м³/c ……………… 0,004 0,006 0,008 0,010 0,012 0,014

h_пот, м ………………. 0,26 0,54 0,92 1,38 1,93 2,57

График h = h (Q) строить не нужно, так как при Q = 0,01 м³/с, h_пот=1,38м. Следовательно, Q = 10 дм³/c.

Проверка подтверждает, что Rе = 23150 > Re_кр.

4. Проверим выполнение условия нормальной работы сифона. "Опасным" сечением, где давление должно быть наименьшим, будет живое сечение в конце горизонтального участка слива как наиболее удаленное от начала движения из всех наиболее поднятых сечений. Урав­нение Бернулли для сечений на поверхности жидкости в верхнем резер­вуаре и "опасного" имеет вид

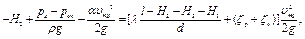(8.3)

где р_оп - абсолютное давление в "опасном" сечении.

5. 0пределим величины α, υ_тр, λ, входящие в уравнение (8.3):

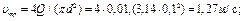
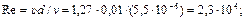
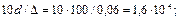
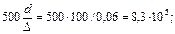
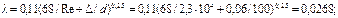
6. Из уравнения (2.2.16.) имеем:

Так как 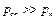, то сифонный слив будет работать.

Пример 8.2.7. Два одинаковых цилиндрических резервуара, расположенные точно друг над другом, заполнены жидкостью до уровня h каждый и имеют донные отверстия площадью f₁ и f₂, коэффициенты расхода которых равны μ₁ и μ₂ соответственно. Отверстия открываются одновременно.

Определить уровень у в нижнем резервуаре в тот момент, когда верхний резервуар будет полностью опорожнен. Найти у в частном случае, когда μ₁ = μ₂ и f₁ = f₂, h=1м.