
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Хотя вода - жидкость маловязкая (h = 10-3 Па∙с, см
Хотя вода - жидкость маловязкая (h = 10-3 Па∙с, см. прил. 4), но квадратичная зона сопротивления сомнительна, так как мала эквивалентная шероховатость труб (∆ = 0,014 мм, см. прил. 1). Поэтому решаем задачу графоаналитическим способом.
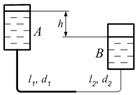
Рис. 8.24
1. Зададимся рядом значений Q и вычислим соответствующие этим значениям hпот для каждого из участков, после чего суммируем их для каждого Q. Полученные результаты приведены ниже, где hобщ = h1+h2.
| Q 103, м3/с … | |||||||
| h1, м………... | 0,18 | 0,36 | 0,60 | 0,89 | 1,23 | 1,62 | 2,06 |
| h2, м……….. | 0,38 | 0,79 | 1,31 | 1,96 | 2,72 | 3,59 | 4,56 |
| hобщ , м……... | 0,56 | 1,15 | 1,91 | 2,58 | 3,95 | 5,21 | 6,63 |
2. По выбранным значениям Q и вычисленным для них hобщ строим гидравлическую характеристику всего трубопровода.
3. Составив уравнение Бернулли для живых сечении, выбранных по уровням жидкости в резервуару получим:
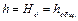
4. Отложив на оси ординат величину Hд = 3 м, находим искомый расход Q = 5,15 дм3/с.
Убедимся, что предположение о квадратичном законе сопротивления было бы ошибочным.


Проверка велась только по d2, так как Re2 > Re1. Ответвления от основной магистрали могут быть замкнутыми (рис. 2.2.31, а) и разомкнутыми (рис. 2.2.31, б). Для замкнутых ответвлений (лупингов - от англ. «петля» - соединенный параллельный трубопровод) справедливы соотношения
 (8.4)
(8.4) 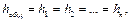 (8.5)
(8.5)
где Qобщ и hобщ - соответственно расход и потери напора на всей разветвленном участке. Следовательно, расход, проходящий через весь разветвленный участок, равен сумме расходов в отдельных ветвях (для рис. 8.24, Qобщ = Q1 + Q2), а потери напора для всего разветвления и в любой его ветви равны между собой.
При аналитическом способе решения задачи на основании анализа исходных данных предсказывается режим движения (для турбулентного движения также зона сопротивления). Затем, используя соотношение (8.4) и (8.5), определяют скорость (или расход) в каждой из ветвей, после чего находят потери напора в одной из них. Принятое предположение подтверждается проверочными расчетами.
Пример 8.2.9.По трубопроводу (см. рис. 8.25, а) перекачивается нефть (ρ = 900кг/м3, ν = 2·10-4 м2/с с расходом Q = 50 дм3/с.

Рис. 8.25. Схемы сложных трубопроводов
а – трубопровод с замкнутым ответвлением (лупингом);
б – трубопровод с разомкнутыми ответвлениями
Определить относительное изменение потерь напора на участке А – B=5 км (d1= 200 мм), если к нему подключить лупинг той же длины (d2 = 260 мм). Трубы сварные новые, местными сопротивлениями пренебречь.
Дата добавления: 2015-04-18; просмотров: 248; Мы поможем в написании вашей работы!; Нарушение авторских прав |