Решение. 1. Определим потери напора на участке A - B до подклю­чения к нему лупинга.

1. Определим потери напора на участке A - B до подклю­чения к нему лупинга.

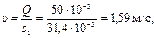
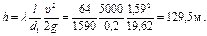
2. Найдем соотношение между Q₁ и Q₂, после подключения лупинга.

Режим движения в трубах должен остаться ламинарным, так как по формуле (8.4) Q₁ и Q₂, меньше Q.

Используя соотношение (1.2.19), с учетом ламинарного режима имеем:

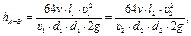
или, проведя сокращения и заменив υ₁ на Q₁, а υ₂ на Q₂ получим (можно было сразу воспользоваться формулой Пуазеля):

, откуда

3. Определим Q₁ и Q₂ и проверим правильность предположения о ламинарном режиме движения.

откуда

Предположение о ламинарном течении подтвердилось.

4. Определим потери напора во всем разветвлении через потери напора в лупинге. По формуле Пуазеля

5. Вычислим относительное изменение потерь напора

Следовательно, после подключения лупинга потери напора на участке А-В уменьшились почти в 4 раза.

При графоаналитическом способе решения строят гидравличес­кие характеристики для каждой из параллельных ветвей и, исходя из соотношений (8.4) и (8.5), путем сложения абсцисс для ряда точек этих кривых, получают гидравлическую характеристику всего разветвленного участка. Для схемы трубопровода на рис. 8.26 такое построение показано на рис. 8.27.

При разомкнутом разветвлении из одного узла (точки соединения разветвляющихся участков трубопровода) решение задачи можно получить, если для каждой из ветвей составить уравнение Бернулли, выбрав сечения в их начале и конце. Например, для ветвей DE и DF (см. рис. 8.25, б), сходящихся в угле D, такие уравнения будут иметь вид:

и

Рис. 8.26. Характеристика сложного Рис. 8.27

трубопровода, имеющего замкнутое

ответвление

Так как z_D и p_D в этих уравнениях общие, то, разрешив уравне­ния

относительно р_D/(pg) и приравняв, можно найти или расходы, идущие в каждую ветвь (Q_E и Q_F в данном примере, если известно Q = Q_E + Q_F), или, при заданных расходах, требуемые диаметры труб каждой из ветвей.

Пример 8.2.10. По временному трубопроводу (рис. 8.27) бензин (Q = 50 дм³/с, ρ = 740 кг/м³, v = 0,55·10^-6 м²/с) подается в стоян­ки для залива цистерн. От основной линии (АВ = l=2 км, d_AB = d = 200 мм) в узле В поток разделяется в линии ВС (l_ВС = l₁ = 100 м, d_BC = d₁ = 125 мм) и BD (l_BD = /₂ = 150 м, d_BD =d₂ = 150 мм). Все трубы сварные умеренно заржавленные, превышение точек С и D над горизонтальной осью трубы АВ: z_С = 10 м, z_D = 13 м.

Определить расходы бензина Q_C и Q_D и избыточное давление р_А,

развиваемое насосом. Местными сопротивлениями и скоростными напорами пренебречь, конечное давление р_С и p_D атмосферное.