
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение неразрывности (сплошности потока) для жидкости
При рассмотрении движения жидкости считают, что в потоке жидкость сплошь заполняет занимаемое ею пространство без образования пустот, т.е. движение жидкости происходит неразрывно. В этом случае справедливо уравнение неразрывности. Дифференциальное уравнение неразрывности – это закон сохранения массы, записанный для элементарного объема жидкости.
Пусть имеем элементарную струйку (рис. 16 а). Возьмем сечение 1-1 с площадью  искоростью движения частиц жидкости и1. Элементарный расход через сечение 1-1 равен:
искоростью движения частиц жидкости и1. Элементарный расход через сечение 1-1 равен:
 ,
,
Затем возьмем сечение 2-2 в этой же струйке с площадью сечения  и скоростью u2. Элементарный расход через сечение 2-2 равен:
и скоростью u2. Элементарный расход через сечение 2-2 равен:
 ,
,
Но по свойству элементарной струйки приток и отток жидкости через ее боковую поверхность невозможен, кроме того, в отсеке 1-2, который сохраняет неизменные размеры, не образуется пустот и не происходит переуплотнений; значит количества жидкости, протекающей в единицу времени через сечения 1-1 и 2-2, должны быть одинаковы, т.е.
 ,
,
Принимая во внимание, что сечения 1-1 и 2-2 приняты произвольно, можно в общем случае для элементарной струйки написать:
 ,
,
Или
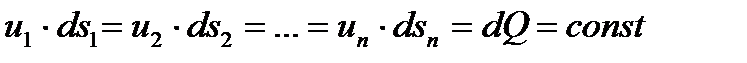
Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: элементарный расход жидкости 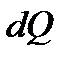 при установившемся движении есть величина постоянная для всей элементарной струйки.
при установившемся движении есть величина постоянная для всей элементарной струйки.
Пусть имеем поток жидкости (рис. 17 б). Взяв в потоке два произвольных сечения 1-1 и 2-2 и представив живые сечения их состоящими из суммы элементарных струек, можно написать:
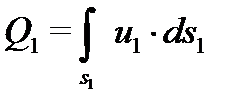 –расход жидкости в сечении 1-1;
–расход жидкости в сечении 1-1;
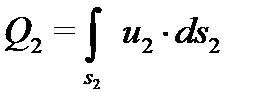 – расход жидкости в сечении 2-2.
– расход жидкости в сечении 2-2.

|  Q1=Q2=const
Q1=Q2=const
|
| а | б |
| а – элементарная струйка жидкости, б – поток жидкости | |
| Рисунок 17 – К уравнению неразрывности или сплошности потока |
Но поскольку скорости касательны к боковой поверхности потока, то в отсек между сечениями 1-1 и 2-2 через боковую поверхность движения жидкости не происходит; не изменяется и объем отсека. Следовательно, в отсек через сечение 1-1 поступает столько же жидкости, сколько за то же время выходит, таким образом 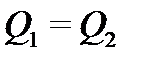 . Но так как сечения 1-1 и 2-2 взяты произвольно, то можно написать, что
. Но так как сечения 1-1 и 2-2 взяты произвольно, то можно написать, что 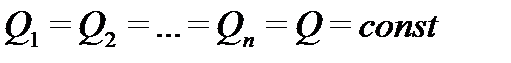 или, выражая расход жидкости в сечениях через среднюю скорость
или, выражая расход жидкости в сечениях через среднюю скорость 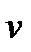 получим:
получим:
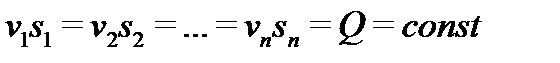
Это и есть уравнение неразрывности (сплошности) для потока жидкости которое читается так: объемный расход жидкости через любое сечение потока при установившемся движении есть величина постоянная.
Из последнего уравнения для двух сечений можно написать:
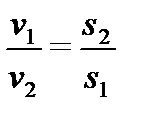 ,
,
т.е. средние скорости потока обратно пропорциональны площадям соответствующих живых сечений [2-4].
Дата добавления: 2015-04-18; просмотров: 278; Мы поможем в написании вашей работы!; Нарушение авторских прав |