Уравнение Бернулли для реальной жидкости

При движении реальной вязкой жидкости вследствие влияния сил молекулярного сцепления между стенкой и жидкостью происходит торможение потока, приводящее к скольжению слоев жидкости друг относительно друга и возникновению напряжений трения между слоями. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием. Все это требует затрат энергии жидкости, поэтому энергия реальной жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока.

Из-за неравномерного распределения скоростей в потоке реальной жидкости приходится вводить в рассмотрение среднюю скорость v, а также среднее значение удельной энергии жидкости в данном сечении. При этом предполагают, что гидростатический напор в пределах сечения есть величина одинаковая для всех точек данного сечения (что абсолютно справедливо для слоя неподвижной жидкости).

В соответствии со сказанным уравнение Бернулли для реальной жидкости имеет следующий вид:

,

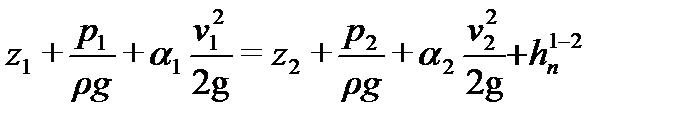В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной удельной энергии (рисунок 21).

Потерянная удельная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости, таким образом, представляет собой баланс энергии в потоке с учетом потерь (рисунок 22).

Рисунок 22 - Демонстрация уравнения Бернулли для реальной жидкости

Из рисунка 22 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрического напора, пьезометрического напора, скоростного напора и потерянного напора между сечениями 1-1 и 2-2.

Потерянный напор складывается из потерь по длине, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями.

В уравнении Бернулли появились безразмерные коэффициенты Кориолиса 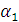и . Коэффициент Кориолиса учитывает неравномерность распределения скоростей по сечению трубопровода и представляет собой отношение действительной кинетической энергии потока жидкости в сечении к кинетической энергии того же потока в этом сечении при средней скорости течения. Во многих практических случаях течение жидкости является турбулентным и коэффициенты Кориолиса принимают равными единице.

Уравнение Бернулли используется при решении большинства задач практической гидравлики [2-4,10].