Практическое применение уравнения Бернулли (измерение расхода жидкости с помощью дроссельных расходомеров)

При применении уравнения Бернулли для решения практических задач гидравлики следует помнить два основных условия:

1) уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения.

2) гидродинамическое давление р и, следовательно, высоту положения z можно относить к любой точке живого сечения, так как для любой точки живого сечения потока при плавно изменяющемся движении есть величина постоянная, что обычно приемлемо для горизонтальных участков трубопроводов.

Разберем применение уравнения Бернулли на примере измерения скорости и расхода жидкости в трубопроводе.

В практической деятельности используются различные способы измерения расхода жидкостей, однако, наибольшее распространение в настоящее время получили нормальные дроссельные расходомеры. Под термином «нормальные» следует понимать объединенные государственными нормалями геометрически подобные, как бы стандартные устройства.

К нормальным дроссельных расходомерам относятся диафрагмы, сопла и трубы Вентури (рисунок 23 а-в) [11,12].

а	б
в

а - диафрагма, б - нормальное сопло, в - труба Вентури

Рисунок 23 - Общий вид в разрезе нормальных дроссельных расходомеров

Диафрагма - это тонкий диск с отверстием круглого сечения, установленный по оси трубопровода.

Сопло – это короткий коноидальный насадок.

Труба Вентури состоит из двух участков – плавно сужающегося (сопла) и постепенно расширяющегося (диффузора).

Идея измерения расхода жидкости дроссельными расходомерами заключается в следующем. В потоке жидкости устанавливается сужающее поток устройство. При движении жидкости по такому каналу поток последовательно перемещается от широкого сечения к узкому. В соответствии с уравнением Бернулли в узком сечении потока, по сравнению с широким сечением доля кинетической составляющей энергии должна быть больше, а составляющей энергии меньше.

Между разностью потенциальных энергий в широком и узком сечениях и величиной кинетической энергии в узком сечении (точнее приращением кинетической энергии) существует однозначная связь, обусловленная законом сохранения энергии (уравнение Бернулли).

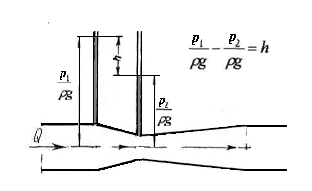
Привлекательным в этой идее является то, что измерение потенциальной составляющей энергии не представляет технической сложности, это можно сделать, измерив, разность пьезометрических напоров с помощью пьезометрических трубок или измерить разность давлений в широком и узком сечениях с помощью манометров или дифференциальным манометром [2-4].

В сечении 1-1 трубы и в суженном сечении 2-2 присоединены пьезометры (рисунок 23 в).

Запишем уравнение Бернулли для выбранных сечений, приняв за плоскость сравнения 0-0 (сечение, проходящее через ось трубы). Тогда , примем α₁ = α₂=…=1.

Тогда уравнение Бернулли запишется так:

или

где h – разница уровней в пьезометрических трубках,

– потери напора между сечениями 1–1 и 2–2,

,

где ζ – коэффициент сопротивления трубы Вентури.

Используя уравнение расхода = , получим

,

где S₂ - площадь широкого сечения, м²;

S₁ – площадь узкого сечения, м².

Совместное решение уравнений приводит к выражению:

,

откуда скорость жидкости в сечении 2-2:

,

Тогда объемный расход жидкости равен:

где К – величина, постоянная для данного расходомера, определяемая опытным путем.

В случае идеальной жидкости ζ = 0, тогда объемный расход идеальной жидкости равен:

Отношение действительного расхода жидкости к теоретическому расходу называют коэффициентом расхода дроссельного расходомера:

,

а с учетом того, что 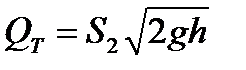, для идеальной жидкости получаем:

,

Величина для реальной жидкости зависит также от критерия Рейнольдса, то есть:

.