
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Основные понятия и определения
Основные понятия и определения
Во многих случаях жидкость движется через грунт по капиллярным поровым каналам, образующимся из-за неполного прилегания частиц породы друг к другу. Движение жидкости через пористую среду называется фильтрацией.
Если движение жидкости в пластах происходит за счет разности давлений в пласте и скважинах без образования свободной поверхности, то такую фильтрацию называют напорной.
Если жидкость при фильтрации образует свободную поверхность в грунте (например, в плотине), то такую фильтрацию называют безнапорной.
Коэффициент пористости m – это отношение объема пор в породе Vп ко всему объему породы V
m = Vп/V.
Коэффициент просветности n – это отношение площади пор в сечении породы Fп ко всей площади сечения породы F
n = Fп/F.
Истинная скорость движения жидкости в пласте vд равна
vд = Q/Fп,
где Q – объемный расход жидкости.
Скорость фильтрации v определяется из условия, что фильтрация происходит как бы через все сечение породы, включая и твердые ее частицы.
v = Q/F.
Проницаемость – это способность породы пропускать через себя жидкость.
Основной закон фильтрации
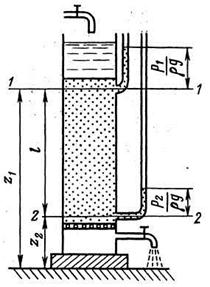 Рисунок 2.13 – Опытная установка
Рисунок 2.13 – Опытная установка
| Через слой песка в вертикальном цилиндрическом сосуде при постоянной разности напоров пропускается вода. Определяя при помощи пьезометров давление в различных по высоте сечениях фильтрующего слоя, изменяя толщину этого слоя и состав песка и измеряя расход фильтруемой воды, Дарси установил основной закон фильтрации, которому подчиняются несжимаемые жидкости при своем движении через грунт Q = k·F·(h/L) – закон Дарси, где Q – объемный расход при фильтрации; F – площадь фильтрации, под которой понимают полное сечение всего фильтрующего слоя, включая как сам грунт, так и поры между отдельными его частицами; h – потеря напора |
h = [z1 + p1/(ρ·g)] – [z2 + p2/(ρ·g)]
L – толщина слоя грунта в направлении фильтрации;
k – коэффициент фильтрации, характеризующий одновременно как фильтрационные свойства пористой среды – грунта, так и физические свойства фильтрующейся жидкости.
Разделив обе части уравнения Дарси на F, получают
v = k·(h/L) = k·i,
где i – гидравлический уклон, то есть потеря напора на единицу длины
i = h/L.
Размерность k – это размерность скорости v. Обычно k измеряют в см/с. При i = 1 k = v, то есть физически коэффициент фильтрации представляет собой скорость фильтрации при единичном гидравлическом уклоне.
Дарси проводил свои опыты с водой. В дальнейшем, при испытании фильтрации других жидкостей, было установлено, что скорость фильтрации обратно пропорциональна вязкости. В связи с этим вязкость жидкости была выделена в отдельный параметр.
В то же время скорость фильтрации стали определять не через перепад напоров, а исходя из разности давлений Δp, соответствующий этому перепаду, то есть Δp = ρ·g·h. Тогда
v = (kп/μ)·(Δp/L) = (kп/μ)·(ρ·g·i),
где kп – коэффициент проницаемости, который характеризует фильтрационные свойства самого грунта;
μ – абсолютная вязкость жидкости.
Коэффициент проницаемости связан с коэффициентом фильтрации соотношением
k/(ρ·g) = kп/μ
Коэффициент проницаемости kп имеет размерность площади, то есть L2. За практическую единицу коэффициента проницаемости принимают проницаемость грунта, которая при площади фильтрации F = 1 см2, толщине слоя фильтрации L = 1 см, абсолютной вязкости фильтрующейся жидкости μ = 1сП и потере давления Δp = 1 кгс/см2 (1ат) пропускает расход жидкости Q = 1 см3/с. Эта единица называется дарси (Д).
1 мД = 1·10-3 Д
1 Д = 1·10-8 см2
1 Д = 1·10-12 м2
Закон Дарси называют линейным законом фильтрации или законом ламинарной фильтрации, так как согласно этому закону расход и скорость фильтрации линейно зависят от потери напора, что является первым признаком ламинарного режима. В большинстве случаев движение жидкости в пористых слоях действительно происходит с очень малыми скоростями, и сечения отдельных пор грунта также очень малы, что делает возможность уподобить фильтрацию ламинарному режиму. В этих случаях применим закон Дарси.
В отдельных случаях закон Дарси нарушается и приведенные выше формулы неприменимы:
1) в крупно-трещиноватых и крупнопористых грунтах, так как скорость движения жидкости увеличивается и наблюдается переход к турбулентному режиму;
2) в весьма мелкозернистых грунтах с очень малыми скоростями, когда начинают заметно сказываться капиллярные силы поверхностного натяжения.
Граница перехода от ламинарного режима к турбулентному устанавливается по критическому значению числа Рейнольдса:
- по Павловскому Re = [1/(0,75m + 0,23)]·(v·dе/ν) и Reкр = 7÷9;
-  по Щелкачеву Re = (10/m0,23)·(v·√kп/ν) и Reкр = 4÷12,
по Щелкачеву Re = (10/m0,23)·(v·√kп/ν) и Reкр = 4÷12,
где ν – кинематическая вязкость жидкости;
dе – эффективный диаметр зерен грунта – это такой диаметр, при котором суммарное процентное содержание фракций более мелкого размера составляет 10% от общего веса.
Для определения скорости фильтрации при турбулентном режиме применяются следующие формулы:
- 

 Краснопольского v = 0,063m1,15· 4√kп· √i / √ρ
Краснопольского v = 0,063m1,15· 4√kп· √i / √ρ
- Смрекера v = c·iα,
где с – коэффициент пропорциональности, определяемый опытным путем;
α– показатель степени, изменяющийся в зависимости от вида грунта в пределах от ⅓ до1.
Параллельно-прямолинейная фильтрация
 Рисунок 2.14 - Параллельно-прямолинейная фильтрация
Рисунок 2.14 - Параллельно-прямолинейная фильтрация
| Рассмотрим случай фильтрации в прямолинейном пласте. Пусть имеется пласт в форме параллелепипеда длиной L, шириной B и толщиной (мощностью) h с непроницаемыми кровлей и подошвой. Контур питания – это изобарическая поверхность, то есть поверхность с одинаковым приведенным давлением в любой точке. Галерея – это условный вертикальный срез пласта, нормальный (то есть перпендикулярный) к линиям тока. За контур питания может быть принято любое живое сечение пласта, где давление известно и при фильтрации считается постоянным. |
За контур питания принята левая граница пласта с давлением рк, за галерею принята правая граница пласта с давлением рг. Этим давлениям соответствуют напоры Нк = pк/(ρ·g) и Нг = pг/(ρ·g). Так как площадь фильтрации (B·h) постоянна по длине пласта, линии тока жидкости будут параллельны друг другу, а поля скоростей и приведенных давлений для любого горизонтального пласта, параллельного линиям тока, будут одинаковыми (поперечных перетоков жидкости в нем нет). Такую фильтрацию называют параллельно-прямолинейной.
Расход, называемый дебитом галереи, равен
Q = (kп/μ)·[(pк-pг)/L]·B·h.
Скорость фильтрации, одинаковая для любого живого сечения пласта, равна
v = (kп/μ)·[(pк-pг)/L].
Возьмем параллельное галерее произвольное живое сечение пласта, отстоящее от нее на расстоянии x. Давление в этом сечении равно р, а напор Нх. Приняв его за контур питания, получим относительно р
р = pг+(Q·μ·x)/(kп·B·h).
Подставив в это выражение значение Q, получают
р = pг+[(рк-рг)/L]·x.
Это и есть закон распределения давления по длине пласта при параллельно-прямолинейной фильтрации. Таким образом, линия падения давлений и соответствующих им напоров представляет собой прямую линию.
При разработке нефтяных месторождений примером фильтрации, близкой к прямолинейно-параллельной, служит фильтрация в полосовой залежи, эксплуатирующейся прямолинейной цепочкой скважин.
Плоско-радиальная фильтрация
Рассмотрим плоско-радиальную фильтрацию несжимаемой жидкости. Пусть скважина расположена в центре кругового пласта толщиной (мощностью) h. Обозначим радиус контура питания Rк, радиус скважины rс, давления на них соответственно рк и рс. Пока скважина не эксплуатируется, в любой точке пласта давление рк, а соответствующий ему статический уровень Нк = pк/(ρ·g). Для того, чтобы жидкость притекала к скважине, необходимо снизить давление на ее забое рс, то есть создать условие рк>рс или Нк>Нс, где Нс = pс/(ρ·g) - динамический уровень жидкости в эксплуатирующейся скважине. Если при этом динамический уровень окажется больше глубины скважины, она начнет фонтанировать, то есть жидкость сможет поступать на поверхность земли только за счет затрат пластовой энергии (гидростатического напора). Если динамический уровень меньше глубины скважины, то добывать жидкость можно только за счет внешних источников энергии (например, насосами).
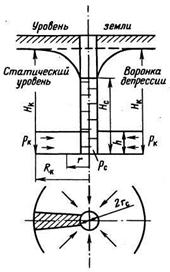 Рисунок 2.15 - Плоско-радиальная фильтрация
Рисунок 2.15 - Плоско-радиальная фильтрация
| Линии тока жидкости в рассматриваемом случае направлены от контура питания к скважине по радиусу пласта, а поля скоростей фильтрации и давлений для любого его горизонтального сечения одинаковы. Такую фильтрацию называют плоско-радиальной. Дебит скважины в этом случае равен Q = [2·π·kп·h/μ]·[(рк-рс)/ℓn(Rк/rс)] – формула Дюпюи, где рк-рс – депрессия, то есть разность пластового и забойного давлений. Формула Дюпюи считается основной при расчетах, связанных с эксплуатацией нефтяных месторождений, а также водяных артезианских скважин. Она также может использоваться и для определения дебита нагнетательных скважин, используемых при заводнении пластов. В этом случае в числителе вместо депрессии рк-рс записывается репрессия, то есть разность забойного и пластового давлений, рс-рк, так как рс>рк. |
Приняв за Rк произвольный радиус r, а за рк соответствующее этому радиусу давление в пласте р, получают
р = рс + [(Q·μ)/(2·π·kп·h)]·ℓn(r/rс).
Подставив в это выражение значение Q, получают
р = рс + [(рк-рс)/ℓn(Rк/rс)]·ℓn(r/rс).
Это и есть закон распределения давления при плоско-радиальной фильтрации. Таким образом, закон распределения давлений (а, следовательно, и динамических напоров) при плоско-радиальной фильтрации логарифмический. Поверхность, образующуюся от вращения логарифмической пьезометрической линии, соединяющей динамические уровни, называют воронкой депрессии.
Из анализа формулы или рассмотрения воронки депрессии видно, что наибольшие потери давления (или соответствующие им потери напора) происходят вблизи от скважины (в призабойной зоне). Это объясняется тем, что при постоянстве расхода (жидкость несжимаема) для любой цилиндрической поверхности радиуса r (Rк ≤ r ≤ rс) максимальная скорость фильтрации будет в зоне малых r. А при фильтрации, также как и при движении жидкости в трубах, с ростом скорости растут и потери давления.
Полученные формулы справедливы для гидродинамически совершенных скважин, то есть скважин, вскрывших пласт на всю его глубину и не отделенных от него обсадной колонной. Если пласт вскрыт не на всю глубину, скважина называется несовершенной по степени вскрытия, если имеется обсадная колонна с перфорированными отверстиями – несовершенной по характеру вскрытия. Возможны и оба вида несовершенства.
Несовершенные скважины дают, как правило, меньший дебит из-за возросшего сопротивления при фильтрации в призабойной зоне. Исключение составляют случаи, когда при перфорации (например, пескоструйной), образуются в пласте каналы, облегчающие приток жидкости.
Несовершенство скважин может быть учтено введением в формулу так называемого коэффициента дополнительного фильтрационного сопротивления С, определяемого по специальным формулам или графикам ([2], стр.192, рис 7.7). В этом случае формула Дюпюи принимает вид
Q = [2·π·kп·h/μ]·[(рк – рс)/ℓn(Rк/rс+С)].
Параллельно-прямолинейная и плоско-радиальная установившаяся фильтрация газа
При фильтрации капельной жидкости ее сжимаемостью обычно пренебрегают, так как она мала, и считают плотность ρ постоянной. Однако для газа такое упрощение непригодно. Как видно из уравнения состояния Клапейрона-Менделеева для совершенных газов,
р/ρ = R·Т,
где R – газовая постоянная;
ρ – плотность газа, прямо пропорциональная давлению;
р, Т – абсолютные давление и температура.
При изотермической фильтрации (Т = const), обычно происходящей в пластах вследствие малых скоростей газа и его теплообмена с породой, уравнение состояния принимает вид:
р/ρ = ра/ρа = const,
где р, ρ – абсолютное давление и плотность газа в любой точке пласта;
ра, ρа – атмосферное давление и соответствующая ему плотность газа.
Для учета сжимаемости фильтрующегося газа Л.С. Лейбензоном была предложена функция Р, названная позже функцией Лейбензона:
Р = ∫ρdp + const.
Функция Лейбензона позволяет переходить от формул для фильтрации несжимаемой жидкости к формулам для фильтрации газа.
Массовый расход газа для любого живого сечения пласта одинаков, а объемный расход будет зависеть от давления. На практике объемный расход (дебит) газовых скважин принято приводить к атмосферному давлению и обозначать Qа.
Qа = [(π·kп·h)/(μ·pа)]·[(pк2 – pс2)/ℓn(Rк/rс)] – формула Дюпюи для газа.
Существует общий способ, используя который легко получить расчетные формулы для дебита газа и законы распределения давления в пласте по соответствующим формулам для несжимаемой жидкости (таблица 2.3).
Таблица 2.3 – Сводная таблица расчетных формул фильтрации
| Вид фильтрации | Вид жидкости | Объемный дебит | Закон распределения давления |
| Параллельно - прямолинейная | Несжимаемая | Q = (kп/μ)·[(pк-pг)/L]·B·h | р = pг+[(рк-рг)/L]·x |
| Газ | Qа = [kп/(2·μ·pа)]·[(pк2-pг2)/L]·B·h | р2 = pг2+[(рк2-рг2)/L]·x | |
| Плоско-радиальная | Несжимаемая | Q = [2·π·kп·h/μ]·[(рк-рс)/ℓn(Rк/rс)] | р = рс + [(рк-рс)/ℓn(Rк/rс)]·ℓn(r/rс) |
| Газ | Qа=[(π·kп·h)/(μ·pа)]·[(pк2–pс2)/ℓn(Rк/rс)] | р2 = рс2+[(рк2-рс2)/ℓn(Rк/rс)]· ℓn(r/rс) |
Как видно из формул закона распределения давления в пласте, для газа при параллельно-прямолинейной фильтрации этот закон параболический (в отличие от линейного для несжимаемой жидкости), а для плоско-радиальной фильтрации газа по сравнению с жидкостью воронка депрессии в призабойной зоне скважины должна быть более крутой. Напомним, что в формулах для газа давления абсолютные, а ра ≈ 0,1 МПа.
Необходимо отметить, что в промысловых условиях закон Дарси при фильтрации нефти почти всегда соблюдается, для газа случаи его нарушения вблизи скважин более часты.
Дата добавления: 2015-04-18; просмотров: 866; Мы поможем в написании вашей работы!; Нарушение авторских прав |