
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания.
    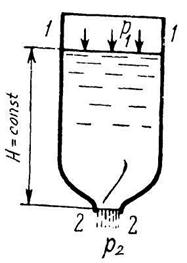 Рисунок 2.7 – Истечение
из отверстия
при постоянном напоре
Рисунок 2.7 – Истечение
из отверстия
при постоянном напоре
| Если жидкость идеальная (невязкая), то есть не оказывает сопротивления при перемещении. В этом случае скорость истечения жидкости называется теоретической, а расход – теоретическим. Составив уравнение Бернулли для сечений 1-1 и 2-2 для идеальной жидкости, и решив его относительно скорости истечения жидкости через отверстие v2, можно получить следующие зависимости vт = √2·g·[H + (p1 – p2)/(ρ·g)] и Qт = f·√2·g·[H + (p1 – p2)/(ρ·g)] При p1 = p2 vт = √2·g·H и Qт = f·√2·g·H, где Н – напор жидкости над отверстием (глубина погружения отверстия); p1 – абсолютное давление на поверхности жидкости; p2– абсолютное давление в пространстве, куда жидкость вытекает; f – площадь сечения отверстия |
Если жидкость реальная (вязкая), то наблюдаются местные потери напора при истечении из отверстия, что приводит к уменьшению скорости движения жидкости и расхода.
Действительная скорость истечения равна
 v = φ·√2·g·[H + (p1 – p2)/(ρ·g)]
v = φ·√2·g·[H + (p1 – p2)/(ρ·g)]
При p1 = p2
 v = φ·√2·g·H,
v = φ·√2·g·H,
где φ – коэффициент скорости – это отношение действительной скорости истечения к теоретической
 φ = v/ vт или φ = 1/√1 + ζ,
φ = v/ vт или φ = 1/√1 + ζ,
где ζ – коэффициент сопротивления отверстия
ζ = 1/ φ2 – 1
Площадь сечения струи меньше площади сечения отверстия, т.е. наблюдается сжатие струи, которое характеризуется коэффициентом сжатия α, представляющим собой отношение площади сжатого сечения струи fсж к площади сечения отверстия f.
α = fсж / f
Действительный расход при истечении из отверстия
 Q = μ·f·√2·g·[H + (p1 – p2)/(ρ·g)]
Q = μ·f·√2·g·[H + (p1 – p2)/(ρ·g)]
 При p1 = p2
При p1 = p2
Q = μ·f·√2·g·H,
где μ – коэффициент расхода, который показывает, насколько действительный расход жидкости при истечении из отверстия уменьшается по сравнению с теоретическим расходом в идеальном случае, т.е. при истечении идеальной жидкости без сжатия струи.
μ = Q/ Qт
Кроме того,
μ = φ·α
При истечении воды из донного отверстия φ = 0,97; α = 0,64; μ = 0,62
Определение коэффициентов истечения (φ, α, μ) опытным путем см. [9], стр.207-209.
Для определения теоретических и действительных скоростей и расходов при истечении из бокового отверстия применяются те же формулы, что и при истечении из донного отверстия, но вместо Н берется Нс – напор над центром тяжести отверстия. Значения коэффициента расхода μ при истечении из бокового отверстия в боковой стенке см. [9], стр.191, табл.40.
Если жидкость вытекает через отверстие в сосуде с постоянным сечением F (вертикальный цилиндрический резервуар), то время полного опорожнения сосуда при p1 = p2 равно

 T = 2·F·√Hн/(μ·f·√2·g),
T = 2·F·√Hн/(μ·f·√2·g),
где F – площадь сечения сосуда;
f – площадь сечения отверстия;
μ – коэффициент расхода;
Hн – начальный напор.
Время, в течение которого уровень жидкости снижается от H1 до H2


 T = 2·F·(√H1 - √H2)/(μ·f·√2·g).
T = 2·F·(√H1 - √H2)/(μ·f·√2·g).
Примечания
1. Формулы для определения времени Т даны при р1 = р2. Если р1 ≠ р2, то необходимо определить приведенный (действующий) напор в начале и в конце истечения
Нпр = Нд = Н + р1/(ρ·g) – р2/(ρ·g)
2. Если в сосуде две жидкости с разными плотностями ρ1 и ρ2, то это необходимо учесть при определении приведенного (действующего) напора.
3. Если площадь сечения поверхности жидкости по мере слива изменяется (горизонтальный резервуар, цистерна), то время слива Т при p1 = p2 см. [2], стр.165-166; [9], стр.195; [11], стр.176.
Расход жидкости через затопленное отверстие при p1 = p2
 |
Q = μ·f·√2·g·ΔH,
где ΔH – разность уровней
ΔH = H1 - H2
Время, в течение которого уровни жидкости в левой и правой частях выравниваются, равно

 T = 2·F1· F2 ·√ΔH/[μ·f·(F1 + F2)√2·g],
T = 2·F1· F2 ·√ΔH/[μ·f·(F1 + F2)√2·g],
где F1, F2 – площади сосудов;
f – площадь отверстия.
Насадок – короткая, обычно длиной ℓ = (3÷4)·d, трубка, приставленная к отверстию в стенке сосуда. Наиболее распространены:
- цилиндрические насадки – внешний и внутренний;
- конические – сходящиеся и расходящиеся;
- коноидальные – криволинейного очертания, имеющие форму сжатой струи.
Расчет насадков проводится по тем же формулам, что и расчет отверстий. Коэффициенты сжатия (α или ε), скорости (φ), расхода (μ) см. [2], стр.172, табл.6.2; [9], стр.202, табл.42; [11], стр.176, табл.12.
Влияние числа Рейнольдса на истечение жидкости
Большинство нефтей и нефтепродуктов отличаются от воды физическими свойствами. Очень часто они имеют более высокую вязкость, чем вода. Вязкость оказывает большое влияние на коэффициенты истечения. Значения этих коэффициентов существенно изменяются в зависимости от числа Рейнольдса.
В результате обработки большого числа опытных данных при истечении жидкости из круглого отверстия с острыми кромками Альтшуль получил характер изменения коэффициентов истечения от числа Рейнольдса ([2], стр.174, рис.6.9; [9], стр.205, рис.153; [11], стр.186, рис.99).
Им же предложены следующие эмпирические формулы для определения коэффициента расхода μ:
§ при Rео < 25 μ = Rео/48
§ при 25 < Rео < 300 μ = Rео/(1,5 + 1,4· Rео)
§ при 300 < Rео < 10000 μ = 0,592 + 0,27/ Rео1/6
§  при Rео > 10000 μ = 0,592+5,5/√ Rео
при Rео > 10000 μ = 0,592+5,5/√ Rео
§ при Rео > 300000 μ практически становится постоянным.
Здесь Rео – число Рейнольдса для отверстия
 Rео = √2·g·Нпр·d/ν,
Rео = √2·g·Нпр·d/ν,
где Нпр – приведенный (действующий) напор над центром тяжести отверстия.
Формулы действительны для истечения из отверстия, когда число Фруда
Fr = v2/(g·L) = 2·H/d > 10,
число Вебера
We = (ρ·v2·L)/σ = (2·H·d·ρ·g)/σ > 200.
По данным Геллера и Скобельцына для наружного цилиндрического насадка коэффициент расхода μ непрерывно возрастает с увеличением числа Рейнольдса для насадка Rен. При
Rен = 10000÷100000 μ становится постоянным. В интервале Rен = 100÷100000 (при ℓ/d = 2÷5) предложена следующая эмпирическая формула
μ = 1 /[1,23+ 58·ℓ/(Rен·d)]
Определение коэффициентов истечения опытным путем

а б
Рисунок 2.8 – Схема установки для определения коэффициентов истечения (а)
и измерений в системе координат xy (б)
Коэффициенты истечения определяют в гидравлических лабораториях на специальных установках. Установка состоит из вертикального сосуда с отверстием в боковой стенке. В этом отверстии перед проведением опыта укрепляется сменная пластинка с подлежащим исследованию отверстием или насадком любой формы. Уровень жидкости в сосуде во время опыта поддерживается постоянным благодаря равномерному поступлению жидкости по трубе А с краном В и наличию сливной линии С.
Уровень замеряется при помощи водомерного стекла или пьезометрической трубки D. Для измерения координат точек вытекающей из отверстия струи жидкости к сосуду прикрепляется горизонтальная металлическая линейка Е с делениями. По ней передвигается ползунок F, несущий на себе вертикальный стержень G, заканчивающийся иглой и также снабженный делениями; это позволяет, подведя острие иглы вплотную к струе жидкости, зафиксировать положение струи в системе координат xy (рисунок 2.7,б).
Непосредственно на установке замеряют диаметр отверстия d и напор над его центром тяжести Н. Рассчитывают площадь сечения отверстия f
f = π·d2/4
Теоретический расход вычисляют по формуле
 Qт = f·√2·g·H.
Qт = f·√2·g·H.
Для определения действительного расхода жидкости Q применяют объемный или весовой способ. Тогда искомый коэффициент расхода равен
μ = Q/Qт.
Теоретическую скорость истечения определяют по формуле
 vт = √2·g·H.
vт = √2·g·H.
Действительная скорость истечения равна
 v = x√g/(2·y),
v = x√g/(2·y),
где x и y – координаты одной произвольно взятой точки струи, которые измеряются горизонтальной металлической линейкой и вертикальным стержнем, заканчивающимся иглой с делениями.
Тогда коэффициент скорости равен
φ = v/vт.
Определив μ и φ и зная, что μ = α·φ, определяют коэффициент сжатия α.
α = μ/φ
Коэффициент сопротивления отверстия равен
ς = 1/φ2 – 1
Давление струи жидкости на преграду
Если струя жидкости, вытекающей из отверстия или насадка, встречает на своем пути твердую преграду (стенку), она давит на эту преграду с некоторой силой, называемой силой удара струи (силой воздействия струи на преграду, силой давления струи).
Величина этой силы зависит от средней скорости и размеров поперечного сечения струи жидкости, формы и размеров преграды и ее расположения по отношению к струе.
1 Удар струи жидкости о симметричную по отношению к струе неподвижную преграду, имеющую вид цилиндрической криволинейной поверхности (рисунок 2.9)
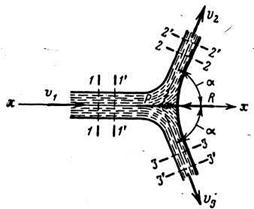 Рисунок 2.9
Рисунок 2.9
| Сила удара струи Р = ρ·v12·f1· (1– cos α), где v1 – скорость истечения струи из отверстия или насадка; f1 – площадь сечения струи; α – угол между горизонтальной осью x и направлением струи после удара. |
2. Удар струи о преграду (пластинку), расположенную нормально (перпендикулярно) к оси струи (рисунок 2.10)
 Рисунок 2.10
Рисунок 2.10
|  Так как cos90° = 0, то Р = ρ·v12·f1. Так как v1 = φ·√2·g·Н, то при φ = 1
Р = 2·ρ·g·f1·Н.
Таким образом, сила давления струи жидкости сечением f1, вытекающей из отверстия под напором н, на расположенную нормально (перпендикулярно) к ней пластинку оказывается в 2 раза больше силы гидростатического давления жидкости Р = ρ·g·f1·Н на ту же площадь f1 при той же глубине погружения Н под свободной поверхностью. Так как cos90° = 0, то Р = ρ·v12·f1. Так как v1 = φ·√2·g·Н, то при φ = 1
Р = 2·ρ·g·f1·Н.
Таким образом, сила давления струи жидкости сечением f1, вытекающей из отверстия под напором н, на расположенную нормально (перпендикулярно) к ней пластинку оказывается в 2 раза больше силы гидростатического давления жидкости Р = ρ·g·f1·Н на ту же площадь f1 при той же глубине погружения Н под свободной поверхностью.
|
3. Удар струи жидкости о преграду, которая представляет собой криволинейную поверхность, отклоняющую набегающую струю жидкости на 180° (рисунок 2.11)
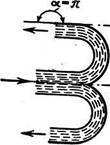 Рисунок 2.11
Рисунок 2.11
| Сила удара струи о такую преграду Р = 4·ρ·g·f1·Н, то есть превышает силу гидростатического давления в 4 раза. |
4. Удар струи о преграду, представляющую собой пластинку, установленную под углом α к оси струи (рисунок 2.12)
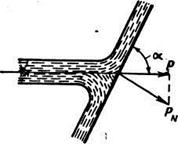 Рисунок 2.12
Рисунок 2.12
| В этом случае, обычно называемом косым ударом, сила давления струи на пластинку в направлении действия струи Р = ρ·v12·f1·sin2α. Сила нормального давления РN = ρ·v12·f1·sin α |
Дата добавления: 2015-04-18; просмотров: 478; Мы поможем в написании вашей работы!; Нарушение авторских прав |