Дифференциальные уравнения покоя жидкости

Рассмотрим покоящуюся жидкость (рис. 6), на которую действует та или иная внешняя объемная сила (не обязательно сила тяжести). Че­рез ф мы обозначим объемную силу, действующую на единицу массы рассма­триваемой жидкости. Обозначим теперь через ф_х, ф_у, ф_г проекции силы ф на оси Ох, Оу, Оz.

В общем случае давление P в разных точках покоящейся жидкости будет
различным: р = f(x, у, z). [15]

Для того чтобы установить связь между давлением P и координатами то­чек, а также величиной ф, поступаем следующим образом.

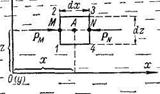
Наметив оси координат Ох и Oz, выделяем элементарный объем покоящейся жидкости в виде прямоугольного параллелепипеда 1—2—3—4, стороны па­раллелепипеда dx и dz, а также dy (перпендикулярную к плоскости чертежа) считаем бесконечно малыми.

В центре параллелепипеда намечаем точку А с координатами х, у и z. Давление в этой точке обозначаем через P. Проведя через точку А линию MN, параллельную оси Ох, можем утверждать, что в общем случае величина гидро­статического давления будет непрерывно изменяться вдоль этой линии. Из­менение величины гидростатического давления, приходящееся на единицу длины линии MN, может быть представлено частной производной.

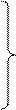P_м = Р - ½ dx 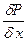[16]

P_N = Р - ½ dx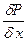

где второе слагаемое правых частей равенств [16] выражает изменение давле­ния р на длине —½ dx.

Далее рассуждаем следующим образом:

а) выясняем все силы, действующие на элементарный параллелепипед;

б) эти силы проектируем на ось Ох; поскольку рассматриваемый параллелепипед находится в покое, то сумму проекций найденных сил приравниваем к нулю, в результате получаем 1-е дифференциальное уравнение;

в) для получения 2-го и 3-го дифференциальных уравнений проектируем все силы, действующие на параллелепипед, соответственно на оси Оу и Oz.

Идя по указанному пути, даем выводтолько для 1-го дифференциального уравнения.

1. Силы, действующие на параллелепипед 1—2—3—4:

а) объемная сила равна

ф (dx dy dz)ρ, [17]

где (dx dy dz)ρ — масса жидкости, образую­щей параллелепипед 1—2—3—4; проекция этой силы на Ох равна:

ф_х (dx dy dz)ρ; [18]

б) поверхностные силы: проекция на ось Ох разности сил давления на грани 1—4 и 2—3 равна нулю; проекция на Ох разности сил давления на грани 1—2 и 3—4 равна:

Р_м — Р n — Рм (dz dy) — p_N (dz dy) = (Р - ½ dx 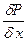)dydz - (Р + ½ dx 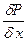) dydz [19]

2. Сумма проекций всех сил на ось Ох равна:

ф_х (dx dy dz)ρ — 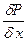(dx dy dz) = 0 [20]

Так выглядит первое уравнение; остальные два пишем по аналогии с пер­вым. Найденные три дифференциальных уравнения (отнесенные к единице массы жидкости) имеют окончательный вид:

Ф_х - 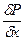= 0 [21]

Ф_y - 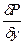= 0

Ф_z - = 0

Эти уравнения были получены Л. Эйлером в 1755г.