Интегрирование дифференциальных уравнений покоя

Умножаем 1-е дифференциальное уравнение [21] на dx, 2-е на dy и 3-е на dz. После этого складываем левые и правые части этих уравнений:

ф_х dx + ф_y dy+ ф_z dz - [22]

Так как давление в точке р есть функция только координат:

p=f(x, у, z),

то можно утверждать, что выражение, входящее в равенство (2-15) и заклю­ченное в скобки, является полным дифференциалом р, т. е. это выражение равно dp. Поэтому уравнение (2-15) можно переписать в виде:

dp =ρ(ф_х dx + ф_уdу + ф_z dz). [23]

Далее рассуждаем следующим образом.

Если левая часть [23] является полным дифференциалом некоторой функ­-
ции, зависящей от координат, то, следовательно, и правая часть [23] должна
являться полным дифференциалом некоторой функции, зависящей от коор-­
динат. Учитывая, что плотность жидкости ρ= const, можно на основании ска­
занного утверждать, что выражение, входящее в [23] и заключенное в скобки,
является также полным дифференциалом некоторой функции, зависящей от
координат. Обозначим эту последнюю функцию через V, причем V=f(х, у, z). Тогда вместо [23] можем написать: dp = ρdV, [24]

где dV = ф_xdx+ ф_уdy + ф_zdz. [25]

С другой стороны, полный дифференциал dV можно представить как сумму частных дифференциалов:

dV = 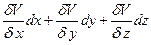[26]

Сопоставляя [25] и [26], видим, что

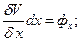
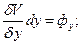
; [27]

Так как V есть функция только координат и так как частные производные ее по координатам дают соответствующие проекции (ф_х; ф_у; ф_z) объемной силы, отнесенной к единице массы, то, следовательно, V является потенциаль­ной функцией. Объемная же сила ф, удовлетворяющая условиям [27] является силой, имеющей потенциал. Из сказанного ясно, что однород­ная несжимаемая жидкость (для которой ρ= const) может находиться в покое под действием таких объемных сил, которые имеют потенциал.

Интегрируя [24], получаем:

p = ρV+C, [28]

где С — постоянная интегрирования.

Чтобы определить С, рассматриваем некоторую точку жидкости, для ко­торой известны р и V:

р = р₀; V = V_o.[29]

Для этой точки [28] перепишется в виде:

P_o= ρV_o + C, [30]

откуда

С = Ро - ρV_O.[31]

Подставляя [31] в [28], получаем:

Р = ρV+ρ_o-pV₀, [32]

или окончательно:

Р = Р_о +ρ (V - V_o). [33]

Формула [33] дает давление в точке для самого общего случая, когда на жидкость действует любая система объемных сил, имеющих потенциал.